[科普中国]-正交投影算子

正交投影算子是把任一元映到该元的正交投影的算子，是希尔伯特空间上特别重要的一类算子。

简介正交投影算子是把任一元映到该元的正交投影的算子。

设M是希尔伯特空间H的闭线性子空间，对任意x∈H，必有分解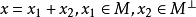，定义算子P如下：Px=x1，即Px是x在M上的投影，称算子P为由H到M上的正交（或直交）投影算子，简称投影（或射影）算子。

性质投影算子P具有下列性质：

p2=P（幂等）；

P有界（事实上有‖P‖=1）；

对一切x,y∈H,(Px,y)=(x,Py)成立（自伴）。反之，H上有界自伴的幂等算子必是投影算子。

正交投影算子与H的闭线性子空间之间成一一对应。

满足PQ=0的两个正交投影算子P和Q称为相互正交的，记为P⊥Q。

应用正交投影算子是希尔伯特空间上特别重要的一类算子，它是希尔伯特空间的很好的几何特征的反映，又是研究其他复杂算子的工具。1

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院