巴拿赫逆算子定理(Banach inverse operator)是关于有界逆算子存在的定理。
简介巴拿赫逆算子定理是关于有界逆算子存在的定理。
设X,Y为弗雷歇空间,T是𝓓(T)⊂X到𝓡(T)⊂Y的闭线性算子,如果T是一对一的,且𝓡(T)是Y中的第二范畴集,则T-1是定义在Y上的连续线性算子。1
特别地,从巴拿赫空间X到巴拿赫空间Y上的一对一有界线性算子T的逆T-1是定义在Y上的有界线性算子。
有界线性算子有界线性算子是泛函分析中一种重要的算子。
设 是从线性赋范空间
是从线性赋范空间 到
到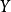 的线性算子。 如果
的线性算子。 如果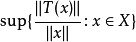 当存在且有限,则称
当存在且有限,则称 是有界线性算子,也就是说
是有界线性算子,也就是说 将
将 中的每个有界集映射为
中的每个有界集映射为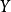 中的有界集。此处
中的有界集。此处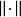 |表示范数,
|表示范数,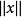 表示
表示 中定义的范数,
中定义的范数, 表示
表示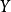 中定义的范数。
中定义的范数。
闭线性算子(closed linear operator)
闭线性算子是一种特殊的线性算子,常直接称为闭算子。连续线性算子必是闭算子,但闭算子不一定是连续算子。根据闭图像定理可知,定义域是闭子空间的闭算子是连续算子。
设X,Y均为Banach空间,T是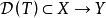 的线性算子。对于任意的
的线性算子。对于任意的 ,若由
,若由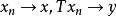 可得
可得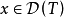 ,且
,且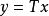 ,则称T为闭线性算子,简称闭算子。
,则称T为闭线性算子,简称闭算子。
本词条内容贡献者为:
李宗秀 - 副教授 - 黑龙江财经学院




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国