奇异性凝聚原理(principle of the condensation of singularities )是有关算子奇异性的定理。
简介奇异性凝聚原理是有关算子奇异性的定理。
设Tmn(m,n=1,2,...)是由巴拿赫空间X到巴拿赫空间Xmn中的有界线性算子,并设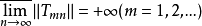 那么存在X中的一个第二范畴集M使X\M是第一范畴的,并且对每个x∈M有
那么存在X中的一个第二范畴集M使X\M是第一范畴的,并且对每个x∈M有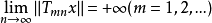
应用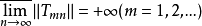 意味着对每个m,存在单位向量列{xmn}使
意味着对每个m,存在单位向量列{xmn}使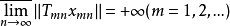 故xmn具有某种奇异性。
故xmn具有某种奇异性。
而上述结论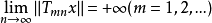 则说明随m,n而变的xmn,可换成固定的x,从而定理称为奇异性凝聚原理。1
则说明随m,n而变的xmn,可换成固定的x,从而定理称为奇异性凝聚原理。1
有界线性算子有界线性算子是泛函分析中一种重要的算子。
设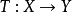 是从线性赋范空间
是从线性赋范空间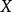 到
到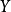 的线性算子。 如果
的线性算子。 如果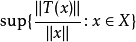 当存在且有限,则称
当存在且有限,则称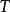 是有界线性算子,也就是说
是有界线性算子,也就是说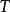 将
将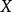 中的每个有界集映射为
中的每个有界集映射为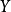 中的有界集。此处
中的有界集。此处 |表示范数,
|表示范数,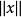 表示
表示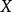 中定义的范数,
中定义的范数, 表示
表示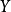 中定义的范数。
中定义的范数。
本词条内容贡献者为:
李宗秀 - 副教授 - 黑龙江财经学院




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国