[科普中国]-共轭线性算子

共轭线性算子（conjugate linear operator）是由线性算子诱导出的共轭空间之间的算子。

简介共轭线性算子是由线性算子诱导出的共轭空间之间的算子。

设X,Y为赋范线性空间，T是X到Y的稠定线性算子。记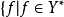𝒟* =，存在g∈X*，使对一切x∈𝒟(T)，g(x)=f(Tx)成立}，这里g由f惟一确定，𝒟*是Y*的线性子空间，在D*上定义算子T*:T*f=g，T*是以𝒟*为定义域的到X*的线性算子，并称为T的共轭算子，也称为T的对偶线性算子或伴随线性算子。

性质当T是有界线性算子时，T*也是有界的，并且‖T*‖= ‖T‖。有界线性算子的共轭算子有如下基本性质：

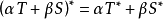（a,β 是数）；

(TS)* = S*T*；

(T-1)* = (T*)-1。

应用当X,Y是内积空间时，T的共轭算子T*是指满足(Tx,y)=(x,T*y)的线性算子。内积空间的共轭算子是线性代数中转置共轭矩阵概念的推广，它与赋范空间上共轭算子的性质的区别仅在于（α,β是数）。特别地，当X=Y是希尔伯特空间时有：

1.若A∈𝓑(X),则A*∈𝓑(X)；

2.A**=A；

3.‖A*A‖= ‖A‖2；

4.ker(A)=𝓡(A*)⊥，ker(A*)= :𝓡(A)⊥，这里的ker(A)为算子A的零空间。

赋范空间中共轭算子是线性代数中转置矩阵概念的推广，所以自然地在研究方程Tx=y时它起着重要作用。1

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院