[科普中国]-派克变换

派克变换（也译作帕克变换，英语：Park's Transformation），是目前分析同步电动机运行最常用的一种坐标变换，由美国工程师派克（R.H.Park）在1929年提出。派克变换将定子的a,b,c三相电流投影到随着转子旋转的直轴（d轴），交轴（q轴）与垂直于dq平面的零轴（0轴）上去，从而实现了对定子电感矩阵的对角化，对同步电动机的运行分析起到了简化作用。

介绍从数学意义上讲，park变换没有什么，只是一个坐标变换而已，从abc坐标变换到dq0坐标，ua,ub,uc,ia,ib,ic,磁链a,磁链b,磁链c这些量都变换到dq0坐标中，如果有需要可以逆变换回来。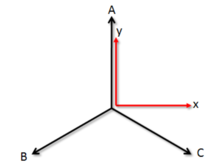

从物理意义上讲，park变换就是将ia,ib,ic电流在α、β轴上的投影，等效到d,q轴上，将定子上的电流都等效到直轴和交轴上去。对于稳态来说，这么一等效之后，iq,id正好就是一个常数了。

从观察者的角度来说，我们的观察点已经从定子转移到转子上去，我们不再关心定子三个绕组所产生的旋转磁场，而是关心这个等效之后的直轴和交轴所产生的旋转磁场了。这样做使得在建立转子回路电磁关系的微分方程时，其系数矩阵成为常数矩阵，而不是随着时间和空间量变化的系数矩阵，这样大大化简了分析发电机、电动机的电磁关系的微分方程。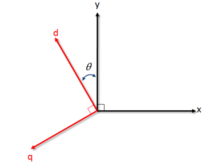

匀速圆周转动的情况下，派克变换就是通过一定的角度旋转变换，把旋转中的向量变为静止直角坐标系里面的量，即将空间静止坐标系代替旋转坐标系。

定义派克正变换：

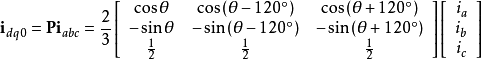
逆变换：

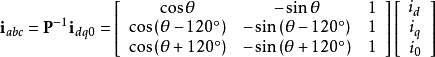
派克变换也作用在定子电压与定子绕组磁链上：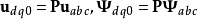

用派克变换化简同步发电机基本方程变换后的磁链方程磁链方程：

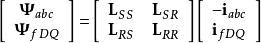
上式中的电感系数矩阵 事实上都含有随时间变化的角度参数，使得方程求解困难。

现对等式两边同时左乘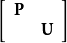，其中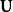为三阶单位矩阵。方程化为：

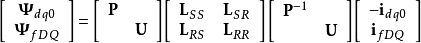
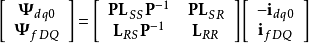
其中 。

① 变换后的电感系数都变为常数，可以假想dd绕组，qq绕组是固定在转子上的，相对转子静止。

② 派克变换阵对定子自感矩阵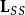 起到了对角化的作用，并消去了其中的角度变量。为其特征根。

③ 变换后定子和转子间的互感系数不对称，这是由于派克变换的矩阵不是正交矩阵。

④ 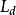为直轴同步电感系数，其值相当于当励磁绕组开路，定子合成磁势产生单纯直轴磁场时，任意一相定子绕组的自感系数1。

变换后的电压方程电压方程：

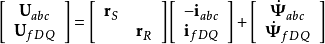
现对等式两边同时左乘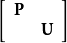，其中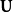为三阶单位矩阵。方程化为：

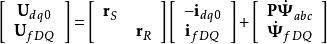
由 ，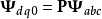

对两边求导，得 ，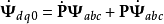

所以

其中 ，令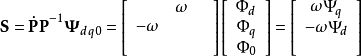

于是有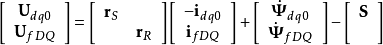

上式右边第一项为绕组电阻的压降，第二项为变压器电势，第三项为发电机电势或旋转电势。

本词条内容贡献者为:

李华青 - 副教授 - 西南大学电子信息工程学院