n 次型亦称n线性型(n-linear operator)。不同的 n 线性算子可对应于相同的 n 次型。
简介n线性算子n线性算子是对n格变元分别是线性的算子。
设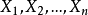 与 Y 是赋范线性空间,
与 Y 是赋范线性空间,
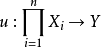 若
若 分别对每一个变元
分别对每一个变元 都是线性的,则称 u 是n线性算子。
都是线性的,则称 u 是n线性算子。
定义设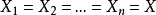 ,如果 n 线性算子
,如果 n 线性算子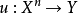 的值
的值 在任意对调xi 与
在任意对调xi 与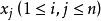 时不变,则称u为对称的n 线性算子,对于 n 线性算子
时不变,则称u为对称的n 线性算子,对于 n 线性算子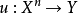 ,令
,令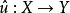 为
为
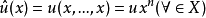 则
则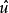 称为u所对应的n次型。
称为u所对应的n次型。
n 次型亦称n线性型。
性质不同的 n 线性算子可对应于相同的 n 次型。
对称的n线性算子与n次型之间一一对应。1
线性型线性型又称线性函数或线性齐次,是域F上的线性空间V到域F上的一个线性映射。
如果f是从V到F的映射,对V的向量x,y,F的元素a,b满足f(ax+by)=af(x)+bf(y),那么f就称为V上的线性型或线性映射。
若e1,e2,...,en是V的一组基,则V的每一个向量x都可以表示成x=x1e1+x2e2+…+xnen,式中xi在F域中,i=1,2,…,n。因此对于V上的线性型f有f(x)=x1f(e1)+x2f(e2)+…+xnf(en)或记成f(x1,x2,…,xn)=a1x1+a2x2+…+anxn,式中f(ei)=ai,i=1,2,…,n。
本词条内容贡献者为:
李宗秀 - 副教授 - 黑龙江财经学院




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国