[科普中国]-巴拿赫矢量丛

巴拿赫向量丛是每点处的纤维均拓扑线性同构于某巴拿赫空间且局部平凡的丛。

简介巴拿赫向量丛是每点处的纤维均拓扑线性同构于某巴拿赫空间且局部平凡的丛。

一个丛指的是三元组ξ=(G,π,B)，其中G和B是拓扑空间，π:G→B是连续满映射。G和B分别称为丛ξ的全空间与底空间，π称为投影。对每点b∈B，π-1(b)称为丛ξ在点b的纤维，记为Gb。设ξ=(G,π,B)是一个丛，称丛ξ=(G,π,B)为巴拿赫向量丛。

性质若存在B的一个开覆盖{Uα|α∈∧}，且对每个α∈∧，对应有某个巴拿赫空间Yα及连续映射τα:π-1(Uα)→Uα×Yα，使得:
1.τα是同胚，且Pατα=π，其中Pα:Uα×Yα→Uα为自然投影；
2.∀b∈Uα，导出映射ταb:π-1(b)→Yα是拓扑线性同构；
3.∀α,β∈A，当Uα∩Uβ≠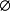时，是从Uα∩Uβ到B(Yα→Yβ)的连续映射，其中B(Yα→Yβ)为从Yα到Yβ的有界线性算子空间。

推广对于巴拿赫向量丛ξ=(G,π,B)，若B是连通的，则上述诸巴拿赫空间Yα彼此拓扑线性同构，这时可将诸Yα取作同一个巴拿赫空间Y。

当B为以E为模的连通的巴拿赫流形时，巴拿赫向量丛ξ=(G,π,B)的全空间G成为以E×Y为模的巴拿赫拓扑流形。进而，若B还是Cr流形，且上述条件3中所述的映射是Cr的，则G是Cr巴拿赫流形，这时称ξ为Cr巴拿赫向量丛。1

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院