[科普中国]-哈密顿圈多面体

哈密顿圈多面体(Hamiltonian circuit polytope)是一种特殊的多面体。它是由哈密顿圈导出的多面体。它的顶点相应一个图上的哈密顿圈的邻接矩阵。

概念哈密顿圈多面体(Hamiltonian circuit polytope)是一种特殊的多面体。它是由哈密顿圈导出的多面体。它的顶点相应一个图上的哈密顿圈的邻接矩阵。因为任何一个图G的哈密顿多面体均为与G同阶的完全图Kn(n为G的阶)的哈密顿多面体的一个面，所以通常所说的哈密顿多面体均指完全图的哈密顿多面体。这时，Kn的哈密顿圈的集合与如下的方程和不等式组解集确定的多面体整顶点的集合之间有一个一一对应关系：

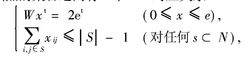
其中，W为Kn关联矩阵，e=(1，1，…，1)为一个n维向量，x=(x1，x2，…，xε)，ε=n(n-1)/2，为ε维向量，t表示向量的转置。由此，哈密顿多面体就是上面方程和不等式组整数解集的凸包。任何一个哈密顿圈均相应旅行售货员问题(参见“旅行售货员问题”)的一个可行解。也可以说，哈密顿多面体为旅行售货员问题所有可行解的凸包。若将Kn用K*n代替，即将Kn的每一边用两个有向边代替，在K*n上考查有向哈密顿圈，则在K*n上的所有有向哈密顿圈的邻接矩阵的凸包称为有向哈密顿多面体。若在旅行售货员问题中，将可行解限制在有向哈密顿圈上，则这时被称为有向旅行售货员问题，或非对称旅行售货员问题。相应地，原旅行售货员问题也称为对称旅行售货员问题。由此，有向哈密顿多面体也可以说是非对称旅行售货员问题所有可行解的凸包。

哈密顿圈问题图论中著名的难题之一。设有一个图，若其上存在一个圈，这个圈包含该图上的每一节点，则称该圈为哈密顿圈，这个图称为哈密顿图。哈密顿圈问题可叙述为：什么样的图为哈密顿图，或者说判断一个图是哈密顿图的行之有效的充分必要条件是什么。目前这一问题尚未解决。关于哈密顿圈的研究，最早是欧拉(Euler，L.)研究骑士(相当于中国象棋中的马)从棋盘上的某一位置出发，走遍所有可能的位置且每个位置只通过一次后，回到原来的位置。而哈密顿(Hamilton，W.R.)研究环游世界的游戏是在欧拉之后近一个世纪，然而却由此开始引起人们对于这个问题的注意。实际上，哈密顿的游戏就是，在一个正十二面体上，从一个顶点开始沿着棱走遍所有的十二个顶点回到原地，使得每一顶点只通过一次。就是在十二面体相应的图上求一个哈密顿圈。若一个图上存在一条路，这条路包含该图上的所有节点，则称该图为可迹图，称这样的路为哈密顿路。若对于一个图上的每一节点，存在一个以该节点为始点的哈密顿路，则称该图为齐次可迹图。一个图被称为哈密顿连通图，若对于这图上任何两节点，存在一条哈密顿路连结这两节点。称一个图为亚哈密顿图，若从这图上去掉无论哪一节点，所得的图都是哈密顿图。称一个图为亚可迹图，若从这图上去掉无论哪一节点，所得的图都是可迹图。

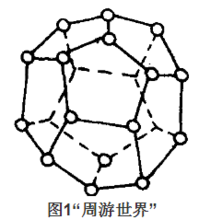
哈密顿图1859年，英国数学家哈密顿提出一种名为“周游世界”的游戏。他用正十二面体(如图1)的20个顶点代表20个大城市，要求沿着棱从一个城市出发，经过每个城市恰好一次，然后回到出发点。

这个游戏曾经风靡一时。为了清楚起见，我们作一个平面图(如图2)，与这个十二面体的顶点和棱所组成的图同构，则图中粗的边组成的圈就是一个所求的路线。我们还可以找到其他的路线。

一般地，在一个给定的图中，若存在一条回路，经过每个顶点恰好一次，则这个回路称为哈密顿回路;若一个图中可以找到一个哈密顿回路，则这个图称为哈密顿图。表面上看哈密顿图的概念与欧拉图的概念非常相似，但两者迥然不同。可以找到一个欧拉图但不是哈密顿图的例子，也可以找到一个哈密顿图但不是欧拉图的例子。

对哈密顿图的判定问题，迄今还没有像欧拉图那样能找到一个很漂亮的充分必要条件。奥尔给出了一个很重要的充分条件：G为简单图，顶点数n≥3，且对每一对不相邻的点u，v，有：

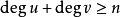这里degu表示与u相关联的边数，则G为哈密顿图。由此还可以得到一个推论：G为简单图，顶点数n≥3，若对G中任何点u，有：degu≥n/2，则G为哈密顿图。

哈密顿英国数学家、物理学家。生于爱尔兰都柏林(Dublin)，卒于都柏林。他自幼才智过人，5岁时能读拉丁语、希腊语和希伯来语，14岁时已学会12种语言。1823年入都柏林三一学院学习。1827年被聘为该校天文学教授，并获得皇家天文学家的称号。1837—1845年任爱尔兰皇家学院院长，并被选为多个科学院和学术机构的成员。1836年获伦敦皇家学会皇家勋章。

哈密顿早年曾精读牛顿(Newton，I.)和拉普拉斯(Laplace，P.-S.)的著作，1822年撰文指出拉普拉斯的《天体力学》中的一个错误，从此开始数学研究。他对数学的主要贡献是创立了四元数理论和发展了变分法和微分方程理论。1835年，撰文详细讨论复数x+iy的性质，进而试图寻找三维“复数”，由此导致创立了形如a+bi+cj+dk(a，b，c，d为实数)的所谓四元数，这是一种不同于实数系和复数系的新数系。四元数的出现，深化了人们对“数”的认识，推动了向量代数、向量分析和物理学的发展。哈密顿用分析的方法研究几何光学，引入了特征函数概念，并利用这一概念和最小作用原理(亦称哈密顿原理)把光学和动力学的问题转化为变分法问题。他建立的动力学方程称为“哈密顿正则方程”，其中以广义坐标和广义动量作为独立变量，代表总能量的函数H称为“哈密顿函数”。这些结果在现代物理学中获得广泛应用。他的主要著作有《四元数讲义》(1853)、《光束论》(1827)和《动力学一般方法》(1834)等。1

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院