对于定向元列{xδ|δ∈△},若存在单调元列{uδ|δ∈△}满足|xδ-x|≤uδ,且∧uδ=0 ,则称 x 为{xδ|δ∈△}的序极限。
简介上确界设 E 是里斯空间,对于 E 中的一族元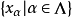 ,若存在 x,使
,若存在 x,使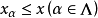 ,则称 x 为
,则称 x 为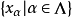 的上界。
的上界。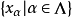 的上界中最小者称为
的上界中最小者称为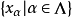 的上确界。用
的上确界。用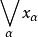 或
或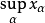 表示。类似地,可定义
表示。类似地,可定义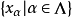 的下确界。1
的下确界。1
定义对于定向元列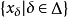 ,若存在单调元列
,若存在单调元列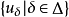 满足
满足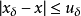 ,且
,且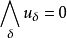 ,则称
,则称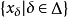 序收敛于 x ,又称 x 为
序收敛于 x ,又称 x 为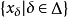 的序极限,记为
的序极限,记为
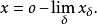
性质序极限如果存在,则必惟一,当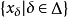 ,
,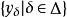 序收敛时,有
序收敛时,有
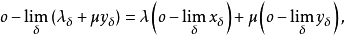
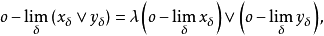
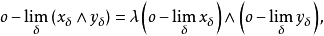 当
当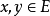 时,如果由
时,如果由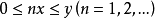 可推出 x=0,则称 E是阿基米德的,则由
可推出 x=0,则称 E是阿基米德的,则由
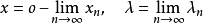 必蕴涵
必蕴涵
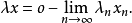
本词条内容贡献者为:
武伟 - 高级工程师 - 天津直升机有限责任公司




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国