[科普中国]-泊松核函数

泊松核函数是不变调和函数的积分表示。齐性有界域上形式泊松核函数是泊松核函数当且仅当D为对称齐性有界。

简介泊松核函数是不变调和函数的积分表示。

记S(D)为有界域D的希洛夫边界，拓扑积D×S(D)上的实值连续函数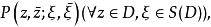如果关于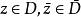为二阶连续可微，关于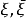在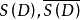上连续，这里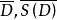表示D及S(X)中点之共轭复数点构成之集合，如果任取S(D)上实值连续函数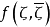，使得为不变调和函数，且当z由D趋于S(D)中点ζ0时，极限为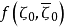，这里ζ为由Cn之欧氏测度在S(D)上的诱导，而V为S(D)的体积，则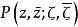称为域D上的泊松核函数。

构造办法利用单复变函数论中构造泊松核函数之办法，很自然的问题是：如果知道域D的柯西核函数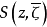，则形式泊松核函数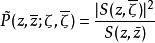在D为对称有界域时，上式为泊松核函数。在一般情形，齐性有界域上形式泊松核函数是泊松核函数当且仅当D为对称齐性有界。1

本词条内容贡献者为:

武伟 - 高级工程师 - 天津直升机有限责任公司