[科普中国]-丹尼尔积分

丹尼尔积分是连续函数空间上的正线性泛函，它由丹尼尔于1919年引入。

简介丹尼尔积分是连续函数空间上的正线性泛函，它由丹尼尔于1919年引入。

丹尼尔积分的意义在于给出一种定义和处理勒贝格积分的方法。

定义设?为集Ω上一族实值函数组成的向量格，即f∈?蕴涵|f|∈?，f∧1∈?；I为?上的正线性泛函，即f,g∈?,α,β∈R1蕴涵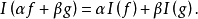又对f∈?,f≥0蕴涵I(f)≥0。如果I满足条件：fn∈?，fn↓0蕴涵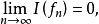或等价地，若由fn∈?，fn↑f∈?必可推出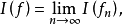则称I为?上的丹尼尔积分。1

丹尼尔表示定理丹尼尔表示定理是体现丹尼尔积分与通常抽象积分之间关系的重要定理。

设?是集Ω上的一族实值函数组成的线性空间，假定?上含有常值函数且关于格运算是封闭的，I为?上的丹尼尔积分，且I(1)=1，则在σ(?)上存在惟一的概率测度μ，使得每个f∈?是μ可积的，且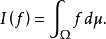

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学