[科普中国]-广义幂级数

广义幂级数是幂级数的推广。广义幂级数的表达式中cn(n=0,±1,...)均为复常数，还可给出不同形式的广义幂级数。

简介广义幂级数是幂级数的推广。

设z0为一有穷点，w2n(z,z0)，w2n+1(z,z0)是分别对应于(z-z0)n，i(z-z0)n（|n|为整数）的广义幂函数，则由以上幂函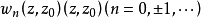数组成的级数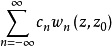称为广义幂级数。这里，cn(n=0,±1,...)均为复常数，还可给出不同形式的广义幂级数。1

收敛半径形如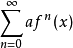的幂级数，其收敛半径求法如下：

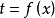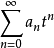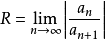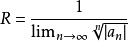令，则级数为，其收敛半径或，故可得：

当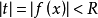时，广义幂级数收敛，此时求出x的范围。

当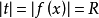时，广义幂级数是否收敛，需要验证，综合以上两步即可得出广义幂级数的收敛域。

幂级数幂级数，是数学分析当中重要概念之一，是指在级数的每一项均为与级数项序号n相对应的以常数倍的(x-a)n（n是从0开始计数的整数，a为常数）。

幂级数是数学分析中的重要概念，被作为基础内容应用到了实变函数、复变函数等众多领域当中。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所