[科普中国]-定义可达性

在编译器理论中，一个指令的定义可达性（Reaching Definition）必然是另外一个指令，而这个指令则是一个没有交错赋值指令的目标变数，举例来说：

例子d1 : y := 3d2 : x := y在d2中，d1为定义可达性，而在下列的范例中：

d1 : y := 3d2 : y := 4d3 : x := yd1在d3不再是定义可达性，因为d2使它不再可能被到达。

作为分析用途定义可达性也可称为数据流分析，它静态的决定在程式码当中哪些定义可以被到达，由于他相当简单，它在教课书当中通常被使用作数据分析的经典范例。数据流汇流运算（data-flow confluence operator）则是使用联集，而他的分析则是正向流动。定义可达性被使用在计算UD链以及DU链。

资料流方程式，给定一个基本区块 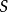在定义可达性：

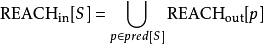
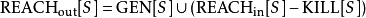
换句话说，定义可达性的集合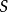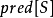为，为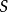的前身，在控制流程图（Control flow graph）中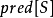，包含所有在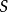区块前的基本区块。定义可达性出来的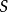，为所有定义可达性自己前身减掉那些被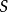剃除掉的变数，再加上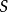产生的新的定义1。

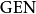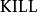我们定义通用的指令及如下：

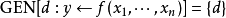
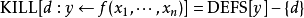
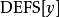为所有赋值给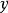变数定义的集合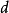，是一个独立的标签附加在赋值的指令，那么定义可达性的值域就是这些指令标签。

工作清单算法通常使用迭代工作列表算法来计算到达定义。

输入：控制流程图CFG =（节点，边缘，进入，退出）

// Initializefor all CFG nodes n in N, OUT[n] = emptyset; // can optimize by OUT[n] = GEN[n];// put all nodes into the changed set// N is all nodes in graph, Changed = N; //Iterate while (Changed != emptyset){ choose a node n in Changed; // remove it from the changed set Changed = Changed -{ n }; // init IN[n] to be empty IN[n] = emptyset; // calculate IN[n] from predecessors' OUT[p] for all nodes p in predecessors(n) IN[n] = IN[n] Union OUT[p]; oldout = OUT[n]; // save old OUT[n] // update OUT[n] using transfer function f_n () OUT[n] = GEN[n] Union (IN[n] -KILL[n]); // any change to OUT[n] compared to previous value? if (OUT[n] changed) // compare oldout vs. OUT[n] { // if yes, put all successors of n into the changed set for all nodes s in successors(n) Changed = Changed U { s }; }}本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所