[科普中国]-简单类型λ演算

简单类型 lambda 演算是连接词只有→(函数类型)的有类型 lambda 演算。这使它成为规范的、在很多方面是最简单的有类型 lambda 演算的例子。

概念简单类型lambda演算是连接词只有→(函数类型)的有类型lambda演算。这使它成为规范的、在很多方面是最简单的有类型lambda演算的例子。简单类型也被用来称呼对简单类型 lambda 演算的扩展比如积、陪积或自然数(系统 T)甚至完全的递归(如PCF)。相反的，介入了多态类型(如系统F)或依赖类型(如逻辑框架)的系统不被当作是简单类型。简单类型 lambda 演算最初由阿隆佐·邱奇在 1940 年介入来尝试避免无类型 lambda 演算的悖论性使用1。

类型简单类型lambda演算的类型构造自基本类型(或类型变量)α,β,γ,…，给定类型σ,τ我们能构造σ→τ。邱奇只使用了两个基本类型，o是命题的类型，ι是个体的类型。这种演算经常只有一个基本类型，通常考虑为o。

→是右结合的:我们读σ→τ→ρ为σ→(τ→ρ)。对每个类型σ我们指派一个数字o(σ)，它是σ的阶。对于基本类型，我们设置o(α)=0，而对于函数类型我们递归的定义o(σ→τ)=max(o(σ)+1,o(τ))。

项要定义有给定类型的lambda项的集合，我们介入定类型上下文Γ,Δ,…，它们是形如x:σ的类型假定的序列，这里的x是变量。我们介入判断Γ⊢t:σ，它意味着t在上下文Γ中是类型σ的项，它们由下列定类型规则给出2:

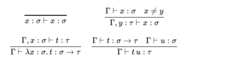
换句话说，
1.如果 x 有类型 σ ，我们知道 x 有类型 σ。
2.在特定上下文中，如果 x 有类型 σ ，而我们有某个不是 x 的 y，则 y 有类型 τ 的事实，和上述上下文一起，允许我们推出 x 有类型 σ 。更加清楚的，向上下文增加一个新值不改变现存的值(假定新值不同于以前的值之一)。
3.在特定上下文中，如果 x 有类型 σ，而 t 有类型 τ ，则我们在同一个上下文中，可以构造lambda 抽象 λ x : σ . t ，它有类型 σ → τ 。
4.在特定上下文中，如果 t 有类型 σ → τ ，而 u 有类型 σ，则我们可以构造表达式 t u，它有类型 τ。这捕获了函数应用的概念。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所