[科普中国]-模糊拓扑线性空间

模糊拓扑线性空间(fuzzy topological vectorspace)是拓扑线性空间的一种推广。它是一种带有与线性结构相适应的模糊拓扑的线性空间。

介绍模糊拓扑线性空间(fuzzy topological vectorspace)是拓扑线性空间的一种推广。它是一种带有与线性结构相适应的模糊拓扑的线性空间。设X是数域K上的线性空间，(X，J)是模糊拓扑空间，若映射：

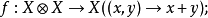
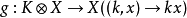均是模糊连续的，则称(X，J)为模糊拓扑线性空间。

模糊拓扑线性空间的概念是1977年凯兹拉斯(Katsaras， A.K.)和刘(Liu， D.B.)引入的。后来，人们对模糊拓扑线性空间的工作，绝大多数是基于(X，J)为满层模糊拓扑空间这一前提，因此，一般当提及模糊拓扑线性空间时，均指(X，J)是满层模糊拓扑空间的情形。1

拓扑线性空间拓扑线性空间是一类具有拓扑结构的线性空间。如果实数域或复数域K上的线性空间E同时是有拓扑τ的拓扑空间，并且线性空间的基本运算x+y和αx(x，y∈E，α∈K)分别作为E×E和K×E到E中的映射按τ是连续的，则称E为(实或复)拓扑线性空间或拓扑向量空间。而τ称为E的线性拓扑或向量拓扑，零元的均衡的邻域全体组成零元的邻域基。满足T1分离公理的拓扑线性空间是完全正则的。2

拓扑线性空间理论是泛函分析的一个重要分支，其基本概念建立于20世纪30年代，而今已经发展成为一门完整的学科，在纯粹数学和应用数学、理论物理、现代力学和现代工程理论中都有广泛应用。

线性空间亦称向量空间。它是线性代数的中心内容和基本概念之一。.设V是一个非空集合，P是一个域。若：

1.在V中定义了一种运算，称为加法，即对V中任意两个元素α与β都按某一法则对应于V内惟一确定的一个元素α+β，称为α与β的和。

2.在P与V的元素间定义了一种运算，称为纯量乘法(亦称数量乘法)，即对V中任意元素α和P中任意元素k，都按某一法则对应V内惟一确定的一个元素kα，称为k与α的积。

3.加法与纯量乘法满足以下条件：

1) α+β=β+α，对任意α，β∈V。

2) α+(β+γ)=(α+β)+γ，对任意α，β，γ∈V。

3) 存在一个元素0∈V，对一切α∈V有α+0=α，元素0称为V的零元。

4) 对任一α∈V，都存在β∈V使α+β=0，β称为α的负元素，记为-α。

5) 对P中单位元1，有1α=α(α∈V)。

6) 对任意k，l∈P，α∈V有(kl)α=k(lα)。

7) 对任意k，l∈P，α∈V有(k+l)α=kα+lα。

8) 对任意k∈P，α，β∈V有k(α+β)=kα+kβ，

则称V为域P上的一个线性空间，或向量空间。V中元素称为向量，V的零元称为零向量，P称为线性空间的基域.当P是实数域时，V称为实线性空间。当P是复数域时，V称为复线性空间。例如，若V为三维几何空间中全体向量(有向线段)构成的集合，P为实数域R，则V关于向量加法(即平行四边形法则)和数与向量的乘法构成实数域R上的线性空间。又如，若V为数域P上全体m×n矩阵组成的集合Mmn(P)，V的加法与纯量乘法分别为矩阵的加法和数与矩阵的乘法，则Mmn(P)是数域P上的线性空间。V中向量就是m×n矩阵。再如，域P上所有n元向量(a1，a2，…，an)构成的集合P对于加法：(a1，a2，…，an)+(b1，b2，…，bn)=(a1+b1，a2+b2，…，an+bn)与纯量乘法：λ(a1，a2，…，an)=(λa1，λa2，…，λan)构成域P上的线性空间，称为域P上n元向量空间。3

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院