[科普中国]-克鲁斯克尔演算法

Kruskal算法是一种用来查找最小生成树的算法，由Joseph Kruskal在1956年发表。用来解决同样问题的还有Prim算法等。

简介Kruskal算法是一种用来查找最小生成树的算法，由Joseph Kruskal在1956年发表。用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪心算法的应用。和Boruvka算法不同的地方是，Kruskal算法在图中存在相同权值的边时也有效1。

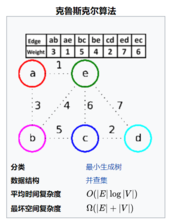
算法步骤新建图G，G中拥有原图中相同的节点，但没有边；

将原图中所有的边按权值从小到大排序；

从权值最小的边开始，如果这条边连接的两个节点于图G中不在同一个连通分量中，则添加这条边到图G中；

重复3，直至图G中所有的节点都在同一个连通分量中。

证明这样的步骤保证了选取的每条边都是桥，因此图G构成一个树2；

为什么这一定是最小生成树呢？关键还是步骤3中对边的选取。算法中总共选取了n-1条边，每条边在选取的当时，都是连接两个不同的连通分量的权值最小的边；

要证明这条边一定属于最小生成树，可以用反证法：如果这条边不在最小生成树中，它连接的两个连通分量最终还是要连起来的，通过其他的连法，那么另一种连法与这条边一定构成了环，而环中一定有一条权值大于这条边的边，用这条边将其替换掉，图仍旧保持连通，但总权值减小了。也就是说，如果不选取这条边，最后构成的生成树的总权值一定不会是最小的。

时间复杂度平均时间复杂度为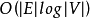，其中E和V分别是图的边集和点集。

算法程序KRUSKAL-FUNCTION(G, w)
F:= 空集合
for each 图 G 中的顶点 v
do 将 v 加入森林 F
所有的边(u, v) ∈ E依权重 w 递增排序
for each 边(u, v) ∈ E
do if u 和 v 不在同一棵子树
then F:= F ∪ {(u, v)}
将 u 和 v 所在的子树合并

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所