[科普中国]-线搜索

最优化问题中，线搜索是一种寻寻找目标函数的局部最小值的近似方法。它是最基础的迭代近似方法之一，另一种是置信域方法。

定义线搜索是一种寻寻找目标函数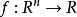 的局部最小值的近似方法。

线搜索近似首先找到一个使目标函数f下降的方向，然后计算x应该沿着这个方向移动的步长。下降方向可以通过多种方法计算，比如梯度下降法，牛顿法和拟牛顿法。计算出的步长不一定是精确的。

方法直接搜索法，这种方法里，必须先把最小值括在一个范围内，也就是说这个算法必须能够找到x1和x2使得要找的最小值在它们之间。接着通过计算这个区间内部的两个点 x3和x4，把区间分成几个子区间，抛弃掉外面两个点中与 x3 和 x4中函数值更小的那个点不相邻的那一个。接下来的每一步中，只需要计算 额外的一个内部的点。在各种划分区间的方法中， 黄金分割法是一种特别简单而高效的方法，它的划分比例在搜索进行中始终保持不变1。

应用以一个梯度法作为例子，其中第四步中使用到了线搜索2。

令迭代计数器 k=0，为最小值做一个初始估计 x0；

重复以下步骤；

计算下降方向pk；

选择以在R上粗略地最小化

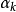
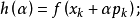
5.更新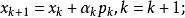

6.直到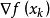小于容忍度。

在第四步的线搜索中算法可以通过解方程 h′(αk)=0，来精确地或者只是通过寻找一个h的充分下降来粗略地最小化 h。前者的一个例子是共轭梯度法。后者被称作不精确线搜索，有很多种实现方法，比如回溯线搜素或者是使用沃尔沃条件。

与其它的最优化方法类似，线搜索也可以跟模拟退火结合以越过一些局部最小值。

本词条内容贡献者为:

鄢志丹 - 副教授 - 中国石油大学（华东）