产业等级质数(Industrial-grade primes)是由亨利·科恩取名的数,表示一整数尚未以严谨的方式证实是质数,但已通过了可能素数测试,像是米勒-拉宾检验(有正的,不可忽略的失效率),或是Baillie–PSW质数测试,还没有任一个合数通过此测试。
简介质数(Prime number),又称素数,指在大于1的自然数中,除了1和该数自身外,无法被其他自然数整除的数(也可定义为只有1与该数本身两个正因数的数)。大于1的自然数若不是素数,则称之为合数1。
产业等级质数简单来说是指一个整数通过了素数测试但在数学上缺乏严格证明。产业等级质数有时会用来代替一些算法中需要的认证质数,像RSA加密算法就需要用户产生大的质数。若数字位数超过100位,证明它们是产业等级质数会比素性测试简单很多。前者可以立即产生,而其不是质数的失效率很低,因此在实务上几乎不可能失效。换句话说,对于于这些数字是质数可以抱持非常高的信心,不过不是一定成立。
素数测试素数问题是一个使得很多数学家着迷的问题。素数就是一个除了 1 和它自身以外不能被其它数整除的数。素数的一个基本问题是如何有效地确定一个数是否是一个素数,即素性测试问题2。素性测试问题不仅在数学上是一个有挑战性的问题,而且在实际中也是非常重要的。例如,很多现代密码学应用通常需要确定一个几百位的素数。如果不采用一些专门有效的方法,即使人们使用运行速度最快的计算机来测试一个 100 位的十进制整数,那么花费的时间将超过宇宙存在的时间。数学家尝试设计对素数的有效测试已经长达两千多年了。Eratosthenes筛法是对于所有素数都有效的最古老的算法,然而它的时间复杂性是输入规模的幂指数,因此在实际中使用它是不合适的。17 世纪的 Fermat 小定理是一些有效素性测试算法的起点,但其逆定理是不满足的。上世纪 80 年代,这个领域的普遍观点是应该存在一个用于素性测试的确定的多项式时间算法,但没有人能给出证明。已经确立了一些素性测试算法,但是它们都存在一些问题。一些算法是非常快速的,但是这些算法会以很小的概率产生一个错误结果;另一些算法是有条件的,如使用了未证明的假设;还有一些算法是确定的也是无条件的,但不能在多项式时间内完成。因此,设计一个在多项式时间内每次都给出一个正确回答的有效算法在计算机科学和数学中都是一个挑战。多年来,研究者们已经尝试了很多方法,包括使用了一些复杂的数学技术,但没有一个成功。
米勒-拉宾素性检验米勒-拉宾素性检验是一种素数判定法则,利用随机化算法判断一个数是合数还是可能是素数。卡内基梅隆大学的计算机系教授Gary Lee Miller首先提出了基于广义黎曼猜想的确定性算法,由于广义黎曼猜想并没有被证明,其后由以色列耶路撒冷希伯来大学的Michael O. Rabin教授作出修改,提出了不依赖于该假设的随机化算法。首先介绍一个相关的引理。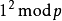 和
和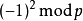 总是得到
总是得到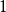 ,称这两个数为1的“平凡平方根”。当
,称这两个数为1的“平凡平方根”。当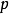 是素数且
是素数且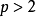 时,不存在
时,不存在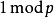 的“非平凡平方根”。为了证明该引理,我们假设
的“非平凡平方根”。为了证明该引理,我们假设 是
是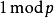 的平方根,于是有
的平方根,于是有
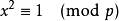
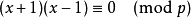
也就是说,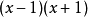 能够整除素数
能够整除素数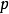 ,根据欧几里得引理,
,根据欧几里得引理,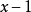 或者
或者 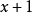 能够整除 p,即
能够整除 p,即 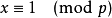 或
或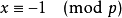 即
即  是
是 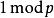 的平凡平方根。
的平凡平方根。
假设 是一个奇素数,且
是一个奇素数,且 。于是
。于是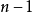 是一个偶数,可以被表示为
是一个偶数,可以被表示为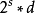 的形式,
的形式,  和
和  都是正整数且
都是正整数且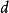 是奇数。对任意在
是奇数。对任意在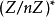 范围内的
范围内的  和
和 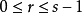 ,必满足以下两种形式的一种:
,必满足以下两种形式的一种:
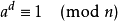
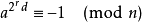
因为由于 费马小定理 ,对于一个素数  ,有
,有
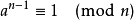
又由于上面的引理,如果我们不断对 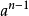 取平方根,我们总会得到 1 或 -1。如果我们得到了 -1,意味着②式成立,
取平方根,我们总会得到 1 或 -1。如果我们得到了 -1,意味着②式成立,  是一个素数。如果我们从未得到 -1,那么通过这个过程我们已经取遍了所有2的幂次,即①式成立。
是一个素数。如果我们从未得到 -1,那么通过这个过程我们已经取遍了所有2的幂次,即①式成立。
米勒-拉宾素性测试就是基于上述原理的逆否,也就是说,如果如果我们能找到这样一个  ,使得对任意
,使得对任意  以下两个式子均满足:
以下两个式子均满足:
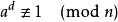
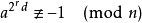
那么 n 就不是一个素数。这样的  称为
称为  是合数的一个凭证(witness)。否则
是合数的一个凭证(witness)。否则  可能是是一个证明
可能是是一个证明  是素数的“强伪证”(strong liar),即当
是素数的“强伪证”(strong liar),即当 确实是一个合数,但是对当前选取的
确实是一个合数,但是对当前选取的 来说上述两个式子均不满足,这时我们认为
来说上述两个式子均不满足,这时我们认为  是基于
是基于 的大概率素数。
的大概率素数。
每个奇合数 都有很多个对应的凭证
都有很多个对应的凭证  ,但是要生成这些
,但是要生成这些  并不容易。当前解决的办法是使用概率性的测试。我们从集合
并不容易。当前解决的办法是使用概率性的测试。我们从集合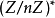 中随机选择非零数
中随机选择非零数 ,然后检测当前的
,然后检测当前的 是否是 n 为合数的一个凭证。如果 n本身确实是一个合数,那么大部分被选择的 a都应该是n的凭证,也即通过这个测试能检测出 n是合数的可能性很大。然而,仍有极小概率的情况下我们找到的 a是一个“强伪证”(反而表明了 n可能是一个素数)。通过多次独立测试不同的 a,我们能减少这种出错的概率。
是否是 n 为合数的一个凭证。如果 n本身确实是一个合数,那么大部分被选择的 a都应该是n的凭证,也即通过这个测试能检测出 n是合数的可能性很大。然而,仍有极小概率的情况下我们找到的 a是一个“强伪证”(反而表明了 n可能是一个素数)。通过多次独立测试不同的 a,我们能减少这种出错的概率。
对于测试一个大数是否是素数,常见的做法随机选取基数 a,毕竟我们并不知道凭证和伪证在 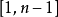 这个区间如何分布。典型的例子是 Arnault 曾经给出了一个397位的合数 n,但是所有小于307的基数 a都是 n是素数的“强伪证”。不出所料,这个大合数通过了 Maple 程序的isprime() 函数(被判定为素数)。这个函数通过检测
这个区间如何分布。典型的例子是 Arnault 曾经给出了一个397位的合数 n,但是所有小于307的基数 a都是 n是素数的“强伪证”。不出所料,这个大合数通过了 Maple 程序的isprime() 函数(被判定为素数)。这个函数通过检测 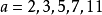 这几种情况来进行素性检验。
这几种情况来进行素性检验。
加密算法在密码学中,加密(Encryption)是将明文信息改变为难以读取的密文内容,使之不可读的过程。只有拥有解密方法的对象,经由解密过程,才能将密文还原为正常可读的内容。加密算法就是加密的方法。加密算法可以分为两类:对称加密和非对称加密在密码学中,加密是将明文信息隐匿起来,使之在缺少特殊信息时不可读。对称加密就是将信息使用一个密钥进行加密,解密时使用同样的密钥,同样的算法进行解密。非对称加密,又称公开密钥加密,是加密和解密使用不同密钥的算法,广泛用于信息传输中。
本词条内容贡献者为:
王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国