[科普中国]-类型居留问题

在简单类型lambda演算中，类型居留问题是如下问题: 给定一个类型τ，是否存在一个λ-项 M 使得对于某个类型环境γ有Γ M：τ? 如果回答是肯定的，则 M 被称为τ的居所。

因为在简单类型的 lambda 演算中类型对应于极小蕴涵逻辑(参见Curry-Howard同构)，一个类型有一个居所，当且仅当它是极小蕴涵逻辑的重言式。

简介在简单类型lambda演算中，类型居留问题是如下问题: 给定一个类型τ，是否存在一个λ-项 M 使得对于某个类型环境γ有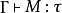 ? 如果回答是肯定的，则 M 被称为τ的居所。

因为在简单类型的 lambda 演算中类型对应于极小蕴涵逻辑(参见Curry-Howard同构)，一个类型有一个居所，当且仅当它是极小蕴涵逻辑的重言式。

Richard Statman证明了类型居留问题是PSPACE-完全性的。1

简单类型λ演算简单类型 lambda 演算( )是连接词只有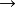 (函数类型)的有类型 lambda 演算。这使它成为规范的、在很多方面是最简单的有类型 lambda 演算的例子。

简单类型也被用来称呼对简单类型 lambda 演算的扩展比如积、陪积或自然数(系统 T)甚至完全的递归(如PCF)。相反的，介入了多态类型(如系统F)或依赖类型(如逻辑框架)的系统不被当作是简单类型。简单类型 lambda 演算最初由阿隆佐·邱奇在 1940 年介入来尝试避免无类型 lambda 演算的悖论性使用。1

柯里-霍华德同构柯里-霍华德对应是在计算机程序和数学证明之间的紧密联系；这种对应也叫做柯里-霍华德同构、公式为类型对应或命题为类型对应。这是对形式逻辑系统和公式计算（computational calculus）之间符号的相似性的推广。它被认为是由美国数学家哈斯凯尔·加里和逻辑学家William Alvin Howard独立发现的。1

对应的起源、范围和结论对应可以在两个层面上看到，首先是类比层次，它声称对一个函数计算出的值的类型的断言可类比于一个逻辑定理，计算这个值的程序可类比于这个定理的证明。在理论计算机科学中，这是连接λ演算和类型论的毗邻领域的一个重要的底层原理。它被经常以下列形式陈述为“证明是程序”。一个可选择的形式化为“命题为类型”。其次，更加正式的，它指定了在两个数学领域之间的同构，就是以一种特定方式形式化的自然演绎和简单类型λ演算之间是双射，首先是证明和项，其次是证明归约步骤和beta归约。

有多种方式考虑柯里-霍华德对应。在一个方向上，它工作于“把证明编译为程序”级别上。这里的“证明”最初被限定为在构造性逻辑中—典型的是直觉逻辑系统中的证明。而“程序”是在常规的函数式编程的意义上的；从语法的观点上看，这种程序是用某种λ演算表达的。所以柯里-霍华德同构的具体实现是详细研究如何把来自直觉逻辑的证明写成λ项。（这是霍华德的贡献；柯里贡献了组合子，它是相对于是高级语言的λ演算是能写所有东西的机器语言）。最近，同样处理经典逻辑的柯里-霍华德对应的扩展可被公式化了，通过对经典有效规则比如双重否定除去和皮尔士定律关联上明确的用续体比如call/cc处理的一类项。

还有一个相反的方向，对一个程序的正确性关联上“证明提取”的可能性。这在非常丰富的类型论环境中是可行的。实际上理论家对推进非常丰富类型的函数式编程语言的开发的动机，已经部分地混合了希望带给柯里-霍华德对应更加显著的地位的因素。1

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所