[科普中国]-二分覆盖

二分图又称作二部图，是图论中的一种特殊模，顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属于这两个互不相交的子集，两个子集内的顶点不相邻。在二分图中寻找最小覆盖的问题为二分覆盖（bipartite - cover）问题。

二分图二分图又称作二部图，是图论中的一种特殊模型。设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

二分覆盖简介在二分图中寻找最小覆盖的问题为二分覆盖（bipartite - cover）问题。二分图是一个无向图，它的n个顶点可二分为集合A和集合B，且同一集合中的任意两个顶点在图中无边相连（即任何一条边都是一个顶点在集合A中，另一个在集合B中）。当且仅当B中的每个顶点至少与A中一个顶点相连时，A的一个子集A'覆盖集合B（或简单地说，A'是一个覆盖）。覆盖A'的大小即为A'中的顶点数目。当且仅当A'是覆盖B的子集中最小的时，A'为最小覆盖。

考察如图所示的具有1 7个顶点的二分图，A={1, 2, 3, 16, 17}和B={4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15}，子集A' = { 1 , 1 6 , 1 7 }是B的最小覆盖。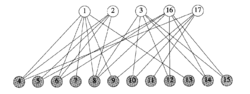

算法思路分析二分覆盖问题是N P -复杂问题。因此可能无法找到一个快速的算法来解决它，但是可以利用贪婪算法寻找一种快速启发式方法。一种可能是分步建立覆盖A'，每一步选择A中的一个顶点加入覆盖。顶点的选择利用贪婪准则：从A中选取能覆盖B中还未被覆盖的元素数目最多的顶点。2

伪代码可以证明：1)当且仅当初始的二分图没有覆盖时，算法找不到覆盖；2)启发式方法可能找不到二分图的最小覆盖。

A' =φ

w h i l e（更多的顶点可被覆盖）

把能覆盖未被覆盖的顶点数目最多的顶点加入A'

i f（有些顶点未被覆盖）失败

e l s e（找到一个覆盖）2

C++代码示例首先计算出集合A和B的大小、初始化必要的双向链表结构、创建三个数组、初始化图遍历器、并创建一个栈。然后将数组C o v和C h a n g e初始化为f a l s e，并将A中的顶点根据它们覆盖B中顶点的数目插入到相应的双向链表中。

为了构造覆盖，首先按SizeOfB递减至1的顺序检查双向链表。当发现一个非空的表时，就将其第一个顶点v加入到覆盖中，这种策略即为选择具有最大New值的顶点。将所选择的顶点加入覆盖数组C并检查B中所有与它邻接的顶点。若顶点j与v邻接且还未被覆盖，则将C o v [ j ]置为t r u e，表示顶点j现在已被覆盖，同时将已被覆盖的B中的顶点数目加1。由于j是最近被覆盖的，所有A中与j邻接的顶点的New值减1。下一个while循环降低这些New值并将New值被降低的顶点保存在一个栈中。当所有与顶点v邻接的顶点的Cov值更新完毕后，New值反映了A中每个顶点所能覆盖的新的顶点数，然而A中的顶点由于New值被更新，处于错误的双向链表中，下一个while循环则将这些顶点移到正确的表中。2

构造贪婪覆盖

bool Undirected::BipartiteCover(int L[], int C[], int& m){// 寻找一个二分图覆盖// L 是输入顶点的标号, L[i] = 1 当且仅当i 在A中// C 是一个记录覆盖的输出数组// 如果图中不存在覆盖，则返回f a l s e// 如果图中有一个覆盖，则返回t r u e ;// 在m中返回覆盖的大小; 在C [ 0 : m - 1 ]中返回覆盖int n = Ve r t i c e s ( ) ;// 插件结构int SizeOfA = 0;for (int i = 1; i