[科普中国]-泰尔森估算

泰尔森估算（英文：Theil–Sen estimator）是通过选择通过成对点的所有线的斜率的中值来稳健地将线拟合到平面中的采样点（简单线性回归）的方法。 它也被称为Sen的斜率估计，斜率选择，单中值方法，Kendall鲁棒线拟合方法，和Kendall-Theil鲁棒线。 它以Henri Theil和Pranab K. Sen命名，他们分别在1950年和1968年以及Maurice Kendall之后发表了关于这种方法的论文。

该估计器可以有效地计算，并且对异常值不敏感。 对于偏斜和异方差数据，它可以比非鲁棒简单线性回归明显更准确，并且就统计功效而言，即使对于正态分布的数据也能很好地与非鲁棒最小二乘法竞争。它被称为“用于估计线性趋势的最流行的非参数技术”。

定义根据Theil（1950）的定义，一组二维点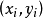 的Theil-Sen估计量是由所有样本对确定的斜率的中值m 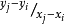。点。 Sen（1968）扩展了这个定义来处理两个数据点具有相同x坐标的情况。在Sen的定义中，人们只采用仅具有不同x坐标的点对定义的斜率的中值。

一旦确定了斜率m，就可以通过将y截距b设置为值yi-mxi的中值来确定来自采样点的线。正如Sen观察到的那样，这个估计量是使得Kendall tau秩相关系数比较xi的值与第i次观测的残差的值近似为零。

斜率估计的置信区间可以被确定为包含由点对[11]确定的线的中间95%的斜率的区间，并且可以通过采样点对并且确定采样的95%间隔来快速估计。连续下坡。根据模拟，大约600个样本对足以确定准确的置信区间。

变化Theil-Sen估计量的变化，Siegel（1982）的重复中值回归，确定每个样本点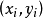 ，通过斜率的中间mi 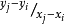那一点，然后将整体估计量确定为这些中位数的中位数。它可以容忍比Theil-Sen估计器更多的异常值，但用于计算它的已知算法较慢。

不同的变体通过其x坐标的等级（具有最小坐标的点与中间坐标上方的第一点配对等）将样本点配对，并计算由这些对确定的线的斜率的中值。分数。

基于加权中值的Theil-Sen估计量的变化也已经被研究，基于x坐标差异更大的样本对更可能具有准确的斜率并因此应该获得更高权重的原则。

对于季节性数据，通过仅考虑属于同一个月或一年中同一季节的样本点对，并找出由下面确定的线的斜率的中值，可以适当地平滑数据中的季节性变化。这种限制性更强的一对。

应用由于具有处理删失回归模型的能力，Theil-Sen估计已应用于天文学。在生物物理学中，Fernandes & Leblanc（2005）建议将其用于遥感应用1，例如从反射数据估计叶面积，因为它“计算简单，置信区间的分析估计，对异常值的鲁棒性，残差和残差的可测试假设”。 ..限制关于测量误差的先验信息“。 为了测量季节性环境数据，例如水质，经季节性调整的Theil-Sen估计变量已被提议优于最小二乘估计，因为它存在偏斜数据时的高精度。在计算机科学中，Theil-Sen方法已用于估计软件老化的趋势。在气象学和气候学中，它已被用于估计风速和发生的长期趋势。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所