费马伪素数(英语:Fermat pseudoprime)是指满足费马小定理的伪素数,也是最重要的一类伪素数。
定义 其定义是:对自然数和一个与其互素的自然数a,如果
其定义是:对自然数和一个与其互素的自然数a,如果 整除a- 1,则称
整除a- 1,则称 是一个以a为底的费马伪素数或者关于a的费马伪素数。最小的费马伪素数是341(=11×31,关于2)。如果
是一个以a为底的费马伪素数或者关于a的费马伪素数。最小的费马伪素数是341(=11×31,关于2)。如果 关于任何与其互素的数都是费马伪素数,则称
关于任何与其互素的数都是费马伪素数,则称 是绝对伪素数(或卡迈克尔数,来自找到第一个绝对伪素数的数学家罗伯特·丹尼·卡迈克尔)。最小的绝对伪素数是561。
是绝对伪素数(或卡迈克尔数,来自找到第一个绝对伪素数的数学家罗伯特·丹尼·卡迈克尔)。最小的绝对伪素数是561。
有人已经证明了费马伪素数的个数是无穷的。有一位数学家如此评论:“对于素数,费马小定理肯定是正确的;但他没说在合数中就不正确。”事实上,费马小定理给出的是关于素数判定的必要非充分条件。
另外,若: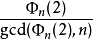 不是素数(如下表中的情况),则它就一定是伪素数。 这些当中包含了所有的费马合数(当n=2),梅森合数(当n=p)及瓦格斯塔夫合数(当n=2p)1
不是素数(如下表中的情况),则它就一定是伪素数。 这些当中包含了所有的费马合数(当n=2),梅森合数(当n=p)及瓦格斯塔夫合数(当n=2p)1
费马伪素数年表1819年,萨鲁斯(Sarrus)发现第一个伪素数341
1903年,马洛(Malo)证明:若n为伪素数,则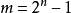 也是一个伪素数,从而肯定了伪素数的个数是无穷的。
也是一个伪素数,从而肯定了伪素数的个数是无穷的。
1950年,发现第一个偶伪素数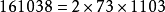 。
。
1951年,皮格(Beeger)证明了存在无限多个偶伪素数。
以2为底的前50个费马伪素数(OEIS中的数列A001567)
|| ||
以任意整数为底的最小费马伪素数(OEIS中的数列A007535)
|| ||
本词条内容贡献者为:
刘燕兵 - 副研究员 - 中国科学院信息工程研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国