概率赋范空间(probabilistic normed space)简称赋范空间,是赋范空间概念的一种推广,是由塞斯特内夫( A.N.Šerstnev)在1962年引入的,概率赋范空间为概率度量空间特例。
基本介绍概率赋范空间是赋范空间概念的一种推广,通常的范数取值于非负实数集,概率范数取值于分布函数集,即实数域R上一类特殊的模糊集所成之集,R上的模糊集F称为分布函数,如果F在R上是单调不减、右连续的,且满足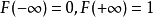 ,
,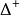 表示满足
表示满足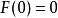 的所有分布函数组成的集合,设X是数域K上的线性空间,τ是三角函数(参见“概率度量空间”),映射
的所有分布函数组成的集合,设X是数域K上的线性空间,τ是三角函数(参见“概率度量空间”),映射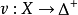 满足以下条件:
满足以下条件:
1.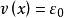 ,当且仅当
,当且仅当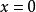 ;
;
2.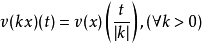 ;
;
3.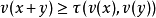 ;
;
则称三元组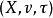 为在三角函数
为在三角函数 下的概率赋范空间,简称赋范空间,ν称为概率范数。若
下的概率赋范空间,简称赋范空间,ν称为概率范数。若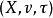 是概率赋范空间,定义
是概率赋范空间,定义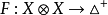 为
为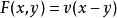 ,则
,则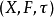 为概率度量空间。
为概率度量空间。
相关介绍定义1 三元组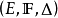 称为Menger概率度量空间,如果
称为Menger概率度量空间,如果
(1)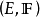 为一个
为一个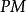 空间;
空间;
(2)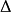 为一个
为一个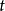 范数(三角范数),满足
范数(三角范数),满足
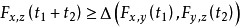
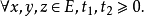
Menger概率度量空间简记为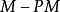 空间。
空间。
定义2 概率线性赋范空间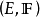 ,如果E是实赋范线性空间,
,如果E是实赋范线性空间,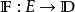 ,满足(记
,满足(记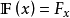 )
)
(1)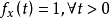 当且仅当
当且仅当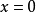 ;
;
(2)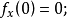 ;
;
(3) ;
;
(4)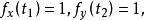 则
则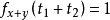 。
。
注 令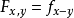 ,易知概率赋范空间为概率度量空间特例。
,易知概率赋范空间为概率度量空间特例。
定义3 称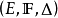 为Menger概率赋值空间,如果
为Menger概率赋值空间,如果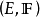 为概率赋范空间,且
为概率赋范空间,且
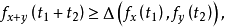 Menger概率赋范空间简记为M-PN空间1。
Menger概率赋范空间简记为M-PN空间1。
概率赋范空间的拓扑结构概率度量空间和概率赋范空间的拓扑结构如下1:
命题1 设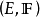 为概率度量空间,定义
为概率度量空间,定义
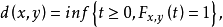 则d是E上的度量,故
则d是E上的度量,故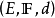 为度量空间。
为度量空间。
命题2设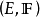 为概率度量空间,且
为概率度量空间,且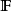 取值于
取值于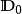 ,
,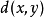 如命题1定义,
如命题1定义,
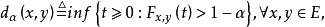 则对任意给定的
则对任意给定的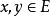 ,
,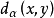 为关于α的减函数(
为关于α的减函数(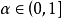 ),且
),且
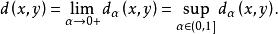
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国