[科普中国]-几何序列

几何序列可分为Ⅰ型几何序列和Ⅱ型几何序列，Ⅱ型几何序列可以看做Ⅰ型几何序列的特殊形式，也可以看作是它的推广形式。Richard Games采用了一种全新的思想理解m序列的周期互相关函数，Klapper、Chan和Goresky在Games的基础上研究了一类称为几何序列的自相关和互相关函数。Ⅱ型几何序列可以看做Ⅰ型几何序列的特殊形式，也可以看作是它的推广形式。

基本介绍Richard Games采用了一种全新的思想理解m序列的周期互相关函数。设GF(2)n是有限域GF(2)上的向量空间，PG(n-1，2)是GF(2)n上的有限射影几何。我们知道任意一个m序列都可以表示成

的形式，这里α是GF(2n)的本原元， 是GF(2n)到GF(2)上的迹函数， 。Games证明了m序列S和 上的超平面

是一一对应的。这样，Games把m序列看成一个有限射影几何上的超平面，则m序列的周期互相关函数等价于超曲面的交点数，然后利用有限射影几何的理论计算出了一些m序列的周期互相关函数。

Klapper，Chan和Goresky在Games的基础上研究了一类称为几何序列的自相关和互相关函数。下面我们给出几何序列的定义1。

*几何序列还有一种定义：称环A的元素序列(un)是几何序列，如果存在A的元素a，使得对任一非零自然数n，有un=aun-1=un-1a. 在此条件下，对任一自然数n，有un=anb，其中b=u0，反之，如果ab=ba，则由前面关系定义的序列(un)是几何序列，它称为以a为公比、以b为首项的几何序列2。

Ⅰ型几何序列定义 设n是正整数，q是素数p的方幂，α是有限域的本原元，

为q元m序列，f是从GF(q)到GF(2)的任意非线性函数，称序列

为Ⅰ型几何序列。

定义2 设是有限域的两个本原元，

f,g是从GF(q)到GF(2)的任意非线性函数，

和

是两个Ⅰ型几何序列。若是

则称序列T和序列S是线性相关的；若

称序列T和序列S是二次相关的。

Klapper等人给出了线性相关和二次相关的Ⅰ型几何序列的互相关函数。但是它们只是下面要介绍的Ⅱ型几何序列的特例，所以这里省略。

Ⅱ型几何序列下面我们研究另外一种形式的几何序列，它既可以看作是定义1中几何序列的特殊形式，也可以看作是它的推广形式。

定义3 设q是素数p的幂，m|n，α是的本原元，

是有限域GF(q)上的GMW序列，f是GF(q)到GF(2)的任意非线性函数，称

为Ⅱ型几何序列，其中

特别地，当r=l时，由于，所以S就退化为Ⅰ型几何序列；在Ⅰ型几何序列中，若取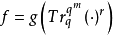，就是Ⅱ型几何序列1。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学