[科普中国]-泰希米勒度量

泰希米勒度量是泰希米勒空间中两点的距离。泰希米勒空间是指黎曼曲面复结构的形变所组成的空间。

简介泰希米勒度量是泰希米勒空间中两点的距离。

设和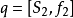是Tg中两点，则称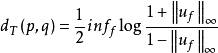为p，q两点的距离，其中f是取自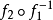的同伦类中所有拟共形映射，uf是f的伸缩商。1

发展泰希米勒证明：在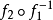的同伦类存在惟一的极值映射达到泰希米勒度量定义中的下确界。

值得一提的是这种复偏差方法可追溯到格勒奇(Grotzsch, H.)的著名变分问题。

泰希米勒空间泰希米勒空间，是指黎曼曲面复结构的形变所组成的空间。理论主要是用拟共形映射为工具来研究黎曼曲面的模问题，这种研究与克莱因群以及低维拓扑问题有一定的联系。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学