[科普中国]-有界平均振动解析函数

有界平均振动解析函数是哈代空间H1的对偶空间中的函数。单位圆盘的解析函数f(z)若能表为一个有界平均振动函数的泊松积分，则称它属于有界平均振动解析函数。

简介有界平均振动解析函数是哈代空间H1的对偶空间中的函数。

有界平均振动函数有界平均振动函数有种种等价描述，其原始定义如下：

对于单位圆周T上的可积函数u，若I是T的子弧，令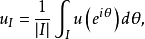这里|I|是I的长度。若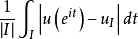对T上的一切子弧I有界，则称u属于BMO（有界平均振动函数的简称）。

有界平均振动解析函数单位圆盘的解析函数f(z)若能表为一个BMO函数的泊松积分，则称它属于BMOA（有界平均振动解析函数的简称）。1

哈代空间哈代空间是单位圆内一类重要的解析函数空间。是由数学家哈代(Hardy，G.H.)在1915年首先提出的。在复分析中，哈代空间（或哈代类）H是单位圆盘或上半平面上的某类全纯函数。高德菲·哈罗德·哈代首先在1915年考虑这类问题。在实分析中，实哈代空间是复哈代空间的成员在实数轴上的边界值。

在较高维的情况，我们可考虑管状域（复数情形）的函数，从而得到相应的定义。哈代空间在数学分析、控制论及散射理论中有所应用。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学