[科普中国]-全纯二次微分

全纯二次微分是一种特殊的二次微分式，是在局部坐标z下表为w=f(z)dz2且在局部坐标变换下不变的微分式。若f是点z的全纯函数，则称w为Sg上的全纯二次微分式。

简介全纯二次微分是一种特殊的二次微分式，是在局部坐标z下表为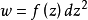且在局部坐标变换下不变的微分式。若f是点z的全纯函数，则称w为Sg上的全纯二次微分式。

由黎曼-罗赫定理可知：Sg上所有全纯二次微分的全体是6g-6维实的向量空间。

应用利用非零全纯二次微分可做出Sg上的局部全纯坐标系，即所谓自然参数。其作法如下：

设p∈Sg，z为p附近的局部坐标，z(p)=0，w=f(z)dz2。若f(z(p))=f(0)≠0，则在原点附近是单射，此处取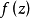为一单值分支，从而在p的邻域内是一局部全纯坐标。

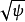若p是w的n阶零点，则存在以原点为中心的圆盘D(0;r)，使得在其内，其中ψ(z)全纯且ψ(z)≠0。取定的一个单值分支；

如n为奇数，则沿切割D(0;r)，然后取zn/2在D(0;r)\I中一个分支；

如n为偶数，则无须切割D(0;r)，总之，

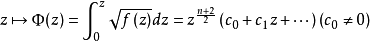是定义于D(0;r)\I的单值函数。可验证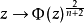是单值且在原点的导数不为0，从而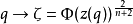可作为p点附近的局部坐标。

推论设0