[科普中国]-三角形化

设M为元素取自交换体K中的n阶方阵，把M三角形化，就是确定一个上三角形矩阵T与一个可逆方阵P，使M=PTP-1，设f为典范地对应于M的Kn之自同态，把M三角形化，就是确定Kn的一个基，使在这个基下对应于f的矩阵是上三角形矩阵1。

基本介绍一般矩阵的三角形化指确定一个上三角形矩阵T与一个可逆方阵P，使方阵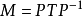。还有下面一种矩阵的三角形化。

如果实对称矩阵

是非奇异的(即如果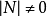 )，则它可分解为两个三角矩阵的积，即 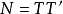，其详细表示是2

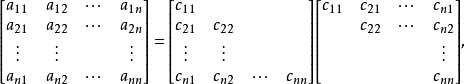矩阵元素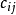 的计算如下(对 )：

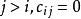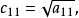
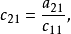
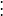
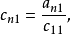
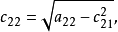
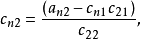
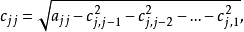
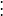
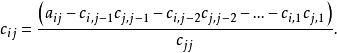
相关介绍三角形矩阵是一种特殊矩阵，数域P上主对角线以下或以上的全体元素都是零的n阶方阵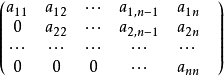 或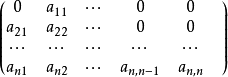 分别称为上三角形矩阵和下三角形矩阵，亦称上三角矩阵和下三角矩阵，统称三角形矩阵。

主对角元全是1的三角形矩阵称为特殊三角形矩阵；主对角元全为零的三角形矩阵称为严格三角形矩阵。

两个n阶上（下）三角形矩阵的和、积以及P中的一个数与上（下）三角形矩阵的乘积仍是上（下）三角形矩阵。

特殊矩阵是假若值相同的元素或者零元素在矩阵中的分布有一定规律，则我们称此类矩阵为特殊矩阵。

在数值分析中经常出现一些阶数很高的矩阵，同时在矩阵中有许多价值相同的元素或者零元素。有时为了节省空间，可以对这类矩阵进行压缩存储。

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学