[科普中国]-突变约定

突变约定(catastrophe convention)是突变理论的一个基本概念，是用来确定在两个或多个平衡位置中的选择准则。设f：M×U→R为一突变模型的势函数，在点u∈U的一个局部系是f|M×{u}→R的一个局部极小点，一个过程是一个可微映射s：U′→M，满足s(u)是一个局部系或-∞，u∈U′，U′是U的开稠密集，一个突变约定是指定一个过程于势函数f，最基本的约定有两种：麦克斯韦约定和完全延迟约定1。

基本介绍突变理论适用于梯度系统，但这时该系统需处于静态或准静态，没有考虑到动力学效应和涨落(系统的状态在平衡位置附近的微小变动)的影响。于是严格来说，根本就不可能实现从一个平衡位置到另一个平衡位置的转换，因为要进行转换需要某种形式的运动。因此，我们要约定这种转换在一定的条件下是可能产生的，并且约定转换进行的方式。

值得指出的是，虽然一个经典的确定性系统(例如势能为的一维谐振子)可以用势的极小点完整地描述，但是一个量子力学谐振子的状态却需要用一个中心点在a的概率分布来描述，这个分布的宽度取决于Schrodinger方程中扩散项的系数。对于这类系统，必须注意涨落水平与势垒高度的相对大小。

考虑用势函数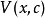描写的系统，这个系统原来处于势函数的一个全局极小点，当参数t变化时，势函数的形状会有所变动，原来的全局极小点可能转化为一个局部极小点而不再是全局极小点，也可能消失。我们需要作某种约定来确定系统在新的势函数下所处的位置，最常用的约定有两种2：

(1)Maxwell约定。系统总是转移到使它的势全局极小的稳定平衡位置。对于参数空间U中的u，当有两个以上的稳定极小值时，s(u)总是选取绝对极小值(即极小值中之最小者)，因此，突变仅出现在势函数有两个以上的绝对极小值时(如图1)1。

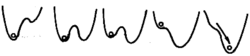
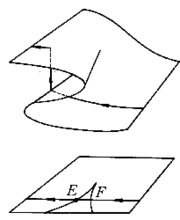
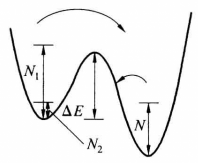
(2)理想延迟约定。也称完全延迟约定，系统留在原来的稳定平衡位置上，直到这个稳定平衡位置消失。当控制参数u在U中变化时，过程s(u)总是尽可能久地连续延伸，直到“无路可走”时为止(如图2)，此时稳定的平衡状态消失在一个退化的临界点，从而使得势fu有退化临界点的u的轨迹起着重要的作用，在齐曼突变机械中，当自由端P在(u，v)平面上移动，从尖点形区域的右方进入而从左方穿出时(如图3)，在点E处(而不是在点F)引起状态曲面M上相应轨迹的跳跃，自由端P移动的轨迹反向移动，从尖点形的左方穿入，从右方穿出(如图4)，相应的M上的过程轨迹不在点E而是在点F处引起突变，这便是“使过程尽可能连续保持”的原则1。

不同突变约定的选用对于梯度动力学系统

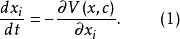
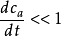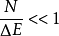当所有的时，采用理想延迟约定比较合理，因为位势变化缓慢，系统无从得知其他极小点的情况。但是对于用分布函数描述的系统，它是否趋于全局极小点。则取决于势垒高度与涨落水平N的相对大小。当时。应采用理想延迟约定，而当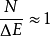时，应采用Maxwell约定(图5)。因此，这两种约定可以被看作两种极限情况。

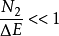：理想延迟约定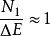；：Maxwell约定。

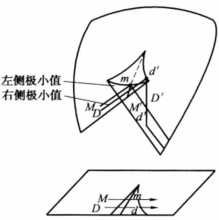
采用不同约定时的分叉集当然也不相同，采用理想延迟约定时的分叉集取决于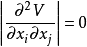这个局部条件，称为局部分叉集，如我们前面所讨论的。而采用Maxwell约定时的分叉集由Clausius-Clapeyron方程确定，称为非局部分叉集。图6示出了对尖点突变的两种分叉集，以及参数变化时系统状态的轨迹。其中D(d)记理想延迟约定，M(m)记Maxwell约定。但实际情况也可能介于这两种极限状况之间，这时分叉集是一个模糊集。

这两种约定都没有考虑动力学效应，下面的例子说明了动力学效应的影响。考虑阻尼振子

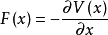其中，并且

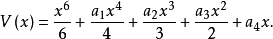
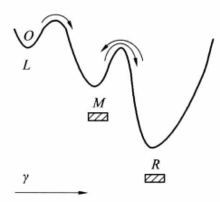
设V(x)的图形如图7所示，原来有三个稳定平衡位置，系统处于左面的稳定平衡位置。当参数变化时，这个平衡位置消失，根据理想延迟约定，系统将进入另一个稳定平衡位置。但究竟是哪一项呢?如果采用

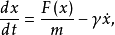那么可以认为系统将静止在中间的平衡位置(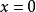)上，因为这里速度为零。但对于式(2)控制的系统，其最终位置实际上取决于γ值的大小和各稳定平衡位置的分布情况。这个问题可以通过对吸引域的形状考虑来加以解决，图3中给出了只考虑γ变化时的示意定性结果，γ越小，交替越频繁。

在突变理论的大多数应用中都选用理想延迟约定，并且不考虑动力学效应2。

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学