[科普中国]-尖点型突变

尖点型突变(the cusp catastrophe)是较简单的且应用广泛的基本突变模型，它的势函数为V(x)=x4+ux2+vx，平衡曲面M的方程为4x3+2ux+v=0，分歧集为8u3+27v2=0，它由DV(x)=4x3+2ux+v=0,D2V(x)=12x2+2u=0组成的方程组消去x得到1。

基本介绍自然界与社会现象中一般的不连续突变问题，都可归属于基本突变模型所刻画，由其特定的几何形状表示，故探讨突变问题就必须按研究基本突变模型的几何形状。

当具有两个控制变量时，最简单的突变模型为尖点型；由于其比较简单，临界曲面也容易构造，且几何直观性强，故属应用最广泛的突变模型2。

尖点突变的几何形状尖点突变，Thorn又称为Rienan-Hugonioc点突变，其势函数为

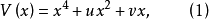故相空间为状态变量x以及u、v两个控制变量构成的三维空间；该势函数的临界点为方程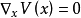的解。故平衡曲面M亦由该方程给出，即

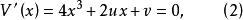其奇点集所相应的方程为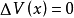，即

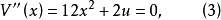将式(2)、式(3)联立求解，消去x则可获得分歧集方程，即判别式△

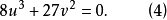
描述平衡曲面的方程式(2)是一个3次方程，该类方程或有一实根，或有3个实根，实根的数目和性质可由判别式△和u、v是否取零值而定。将平衡曲面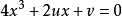绘出，如图1所示。设系统的状态是以x、u，v为坐标的三维空间中的一点所代表，则相点必定位于该曲面上，且总是位于曲面的顶叶或底叶，因为中叶是对应于不稳定平衡2。

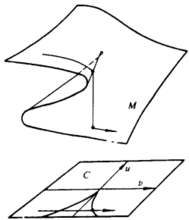
平衡超曲面M在控制平面C即u-v中的投影是一种拓扑变换或映射，可用f表示为

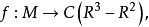即

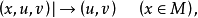u、v的平稳变化一般都引起x的平稳变化。仅当控制点(u，v)越过分歧集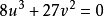时，将使x产生不连续的突变，亦即如果相点恰好在M曲面终止的边缘上(曲面回折面形成中叶处)，则它必定跳跃到另一叶上，这引起x的突变，并产生滞后现象。尖点之中有两个极小点，它们被一个极大点分隔，而尖点之外只有一个极小点，如图1所示。另外，由于当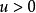时，v的变化只引起x的光滑变化，故称为正则性态。相应地称v为正则因子。但当u减少到负值时，即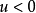时就分裂了M，出现折叠，x的变化不再连续，故称u为剖分因子2。

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学