基本突变(elementary catastrophe)是突变理论的主要研究对象与基本内容,指那些现象被一个势函数所描述,且其外参数不超过4时,势函数的分类。托姆(R.Thom)在分类定理与开折理论的基础上创立的7种基本的突变模型是突变理论的主要内容。从数学上来说,它们的势函数即奇点分类定理中的奇点的万有开折;从模型的意义来说,它们是外部控制参数在1与4之间的稳定静模型必等价于其中之一1。
基本介绍在客观世界中,各种系统的状态变化大部分都是连续渐变的,对于这种连续过程的定量理论描述就是微积分和微分方程等数学理论;而自然界中,同样存在另一类非连续的过程,即突变过程。这种突变现象如何用数学形式来表述,是很值得研究的问题。
1969年法国数学家托姆(R.Thorn)首先提出了突变理论(Catastrophe Theory),并于1975年出版了这方面的一本专著《结构稳定性和性态发生学》。几乎同时,英国数学家齐曼(E.C.Zeeman)对突变理论也做了许多重要工作,于是突变理论便成了数学中的一个分支。
实质性状态变量不多于2,余维数不大于4时,可能出现的所有突变类型,托姆称它们为初等突变或基本突变。
k次截断与k次确定
一个单变量函数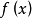 在原点的Taylor级数展开为
在原点的Taylor级数展开为
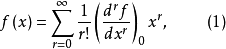 把展开式中k次项以后的项去掉,所剩下的项称为k次截断,用符号
把展开式中k次项以后的项去掉,所剩下的项称为k次截断,用符号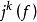 表示为
表示为
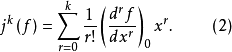 例如,
例如,
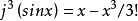
如果一个函数与任何有同样k次截断的函数类型相同,则它被称为k次确定。上述定义同样适用于多变量系统2。
突变的基本类型下面讨论突变生成函数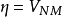 的拓扑等价形式。首先讨论只有一个实质性状态变量x的情况,因为x为实质性状态变量,必然有
的拓扑等价形式。首先讨论只有一个实质性状态变量x的情况,因为x为实质性状态变量,必然有
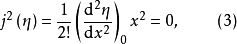 设
设
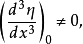 则有
则有
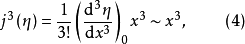 或写为
或写为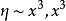 是折叠突变生成函数的拓扑等价形式,或称它为折叠突变核。它的余维数为1,因为只有—个方程
是折叠突变生成函数的拓扑等价形式,或称它为折叠突变核。它的余维数为1,因为只有—个方程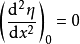 。如果三次截断也为零,即
。如果三次截断也为零,即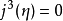 ,而
,而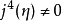 ,则有
,则有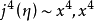 是尖点突变核。因为存在两个方程
是尖点突变核。因为存在两个方程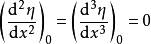 ,它的余维数为2。以此类推,可找到余秩数为1和余维数小于或等于4的其他两类突变核2。
,它的余维数为2。以此类推,可找到余秩数为1和余维数小于或等于4的其他两类突变核2。
假定一个系统的动力学可以由一个光滑的势函数导出,托姆用拓扑学的方法证明了:可能出现性质不同的不连续构造的数目并不取决于状态变量的数目(这可能很大),而取决于控制变量的数目(这可能很小)。按照托姆突变理论分类定理,自然界和社会现象中的大量不连续现象,可由某些特定的几何形状来表示。只要控制参量的个数不超过5,那么,按某种意义的等价性分类,总共有11种突变类型。但发生在三维空间和一维时间的四个因子控制下的形形色色的初等突变,概括起来只有7种性质的基本类型,如表1所示。这些数学模型具有高度的概括性和普遍性,其证明是相当困难的,但掌握证明的结果却是比较容易的2。
|| || 表1 基本突变类型
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国