[科普中国]-完美图

完美图(perfect graph)是一种特殊的简单图，若图G的任意一个节点导出图H的色数χ(H)等于H的团数，则称G是χ完美图。若图G的任意一个节点导出子图H的独立数α(H)等于H的团划分数，则称G是α完美图，弱完美图猜想：G是χ完美图的充分必要条件是G为α完美图；或等价地，完美图的补图是完美图。由于它已获证，并称为完美图定理，这就允许不必区别χ完美图和α完美图，而统称为完美图，强完美图猜想：G是完美图当且仅当G和G的补图GC都不含长大于3的奇圈作为节点导出子图，这个猜想至今尚未得到证明1。

基本介绍我们已经知道，对任一个图，有如下一些基本参数：

点无关数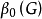，即最大点无关集的点数；

团数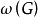，即最大团的点数；

点色数；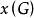

还有另一个参数：

团覆盖数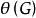，即这样的最小的k，使G中存在k个团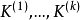，有。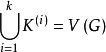

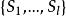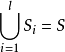如果我们给了一个集合S的一个子集族，使，则称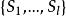覆盖了S，利用“覆盖”的语言，那么点色数就是覆盖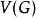所需要的点无关集的最小个数；而团覆盖数就是覆盖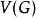所需要的团的最小个数。

以上这些参数之间有着紧密的联系。若Gc是G的补图，则有

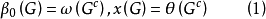这是因为在G与Gc中，点无关集和团是一一对应的．。此外，显然有

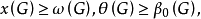这是因为任一个团和任一个点无关集最多有一个公共点。

1960年Berge引进了完美图的概念。

称图G是x完美图，如果

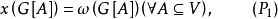称图G是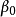完美图，如果

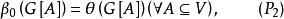若图G既是x完美图，又是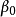完美图，则称G是完美图2。

相关性质定理1961年，Berge提出了如下猜想2：

一个图是完美的充分必要条件是它为x完美图(或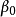完美图)，即。

1972年，Lovász，Fulkerson相继独立地证明了这个猜想。

因为对任意的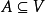，有

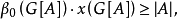
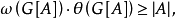所以当G满足(P1)或(P2)时，显然也满足

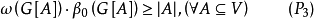由(1)推知：

G满足(P1)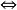Gc满足(P2)；

G满足(P3)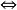Gc满足(Ps)，

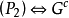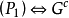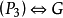所以假如我们能够证明，则G满足满足满足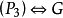满足满足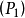，从而就证明了。

因已知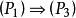，所以证明上述Berge猜想的关键是去证明。

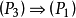现在我们给出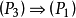的证明。

首先引入图上的一种运算——倍点运算。

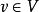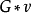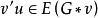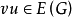对任意的，用表示这样的一个图：在G中增加一个新点v'，并且当且仅当，我们说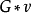是由G通过倍点运算得到的。

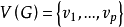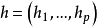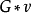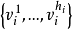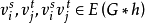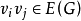设，设是任一非负整数向量，以表示这样的一个图： 用点无关集代替vi，对任意的当且仅当，当某个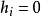时，则意味着从G中丢去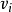，因此，对任意的(0，1)向量h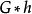，与G的生成子图对应。

引理1 设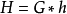，则

(1)若G满足(P1)，则H满足(P1)；

(2)若G满足(P2)，则H满足(P2)。

引理2(Fulkerson，1971；Lovász，1972)设G满足(P2)，令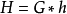，那么由G满足(P3)可推出日满足(P3)。

引理3(Lovász，1972)若G满足(P3)，则G满足(P1)。

由引理3，就可推得

定理 对任意图G，

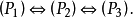
推论1 图G是完美图当且仅当Gc是完美图。

推论2 图G是完美图当且仅当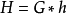是完美图。

由前面我们已经知道，若G或Gc包含一个生成子图，则G不是完美图。

Berge关于完美图的第二个猜想(强完美图猜想)是

猜想 若G或Gc不含生成子图，则G是完美图。

迄今已知这个猜想对许多图类是成立的，如三角图2。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学