[科普中国]-择近原则

设F(X)表示论域X上的所有模糊集组成的集合，如果映射σ： F(X)×F(X)→[0，1]具有以下性质：1.σ(A，A)=1;2.σ(A，B)=σ(B，A);3.当A⊂B⊂C时，有σ(A，C)≤σ(B，C)，则称σ为贴近度。符合上述条件的贴近度有各种不同的形式，可根据具体情况加以选用。设A1，A2，…，An是n个不同的模型，对于给定的B，若σ(B，Ai0)=maxi≤nσ(B，Ai)，则认为B与模型Ai0最贴近，这称为择近原则，它用于模式识别中1。

基本介绍设论域U上有n个模糊子集，它们各代表了n个不同的模式(标本)，是待识别的模糊集，问B应归属于哪一个模糊子集?通常可使用择近识别原则进行判别，它是建立在贴近度概念之上的一种识别法则，也是模糊识别最重要的法则之一。

**择近原则：**设论域U上有n个模糊子集，对于任何，如果：

则认为模糊集B应相对归属于模糊集，其中为B与Ai的贴近度。

显然，该法则是要从一群已知的模糊集中，找到与模糊集B最为相似的一个，并最终认定B的隶属应归于与B最为相似的那个模糊集，这便是择近识别原则的本质所在2。

例题解析【例1】植物群落的演替分为Ⅰ、Ⅱ、Ⅲ、Ⅳ四个阶段，植物群落类型分为St、Ag、Ar、Co四种，各植物群落类型对各阶段的隶属度如下面的矩阵所示：

首先求出各行的最大值如上所示，这些最大值分别处在矩阵的第1、2、3、4列的对角线上，因此按照最大隶属度识别原则，各阶段的植物群落可以分别被命名为St、Ag、Ar、Co型，并称其是各阶段的优势种。

在各阶段中，称与该阶段的优势种最为贴近(即贴近度最大)的种群(植物群落)称为亚优势种。

如果采用黎曼第一贴近度公式进行计算各阶段之间的贴近度，则各植物群落之间的贴近度计算过程如下。

对于第Ⅰ阶段有

该矩阵的计算是由上述隶属度矩阵的第1行元素得到的，例如第2行第3列元素的计算过程为：0.1339/0.2026=0.6609，即用隶属度矩阵中第1行的第2个数和第3个数用较小数除以较大数得到，计算完所有贴近度之后，再求得这些贴近度中的最大值，显然最大值为0.6609，它是Ag与Ar的贴近度。可见，在第Ⅰ阶段中，Ag与Ar最为贴近。但第Ⅰ阶段的优势种为St，而第Ⅰ阶段中与St最为贴近(贴近度为0.3148)的是Ag，因此第Ⅰ阶段的亚优势种应为Ag，而Ar会最贴近Ag进行演替下去，同理其他三个阶段的贴近度为2：

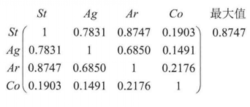
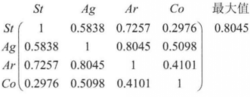
在第Ⅱ阶段中， St与Ar最为贴近，但第Ⅱ阶段的优势种为Ag，而第Ⅱ阶段中与Ag最为贴近(贴近度为0.7831)的是St，因此第Ⅱ阶段的亚优势种应为St，而Ar会最贴近St进行演替下去。

在第Ⅲ阶段中，St与Ag最为贴近，但第Ⅲ阶段的优势种为Ar，而第Ⅲ阶段中与Ar最为贴近(贴近度为0.4416)的是Ag，因此第Ⅲ阶段的亚优势种应为Ag，而St会最贴近Ar进行演替下去。

在第Ⅳ阶段中，Ag与Ar最为贴近，但第Ⅳ阶段的优势种为Co，而第Ⅳ阶段中与Co最为贴近(贴近度为0.5098)的是Ag，因此第Ⅳ阶段的亚优势种应为Ag，而Ag会最贴近Ar进行演替下去2。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学