信道的香农极限(或称香农容量)指的是在会随机发生误码的信道上进行无差错传输的最大传输速率。它的存在是香农定理在带宽有限的信道上的一个结论。
简介信道的香农极限(或称香农容量)指的是在会随机发生误码的信道上进行无差错传输的最大传输速率。它的存在是香农定理在带宽有限的信道上的一个结论。1
有噪信道编码定理在信息论里,有噪信道编码定理指出,尽管噪声会干扰通信信道,但还是有可能在信息传输速率小于信道容量的前提下,以任意低的错误概率传送数据信息。这个令人惊讶的结果,有时候被称为信息原理基本定理,也叫做香农-哈特利定理或香农定理,是由克劳德·艾尔伍德·香农于1948年首次提出。
通信信道的信道容量或香农限制是指在指定的噪音标准下,信道理论上的最大传输率。
根据香农1948年的陈述,本定理描述了在不同级别的噪音干扰和数据损坏情况下,错误监测和纠正可能达到的最高效率。定理没有指出如何构造错误监测的模型,只是告诉大家有可能达到的最佳效果。香农定理可以广泛应用在通信和数据存储领域。本定理是现代信息论的基础理论。香农只是提出了证明的大概提纲。1954年,艾米尔·范斯坦第一个提出了严密的论证。
香农定理假设一个有噪音的信道,信道容量为C,信息以速度R传送,如果
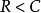
那么就存在一种编码技术使接收端收到的错误达到任意小的数值。这意味着理论上,有可能无错误地传送信息直到达到速度限制C。
反过来同样重要。如果
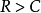
那么想达到任意小的错误率是不可能实现的。因此,在传送速度超过信道容量的时候,可靠传输信息是不能被保证的。定理并没有指出在什么特殊情况下速度和容量相等。
简单的流程如"重复发送数据3遍,用一个投票系统在数据不一样的时候选择3个里面相同的那两个的值"是低效的错误纠正的方式,不能保证数据块能完全没有错误地传送。先进一些的技术如里德-所罗门码编码技术和更现代一些的Turbo码、LDPC码等编码技术更逼近香农限制,但是计算复杂度很高。1
理想加白噪声情况下香农限考虑数据率、噪声以及误码率的关系。噪声的存在会破坏一个或多个比特。假如数据率增加,那么这些比特会变短,因而给定的噪声模式会影响更多个比特。于是,给定一个噪声值,数据率越高则误码率也越高。所有的这些概念可以通过香农公式清楚联系在一起,此公式由数学家克劳德·艾尔伍德·香农(Claude Elwood Shannon,1916-2001)推导得出的。
如刚才所描绘的,数据率越高,无用的噪声会带来更严重的破坏。在噪声存在的情况下,给点一个噪声值,我们能够通过提高信号强度来提高正确接收数据的能力。在这一推导过程中涉及的主要参数是信噪比(SNR或S/N),它是指在传输过程中某一点的信号功率与噪声包含功率之比。通常信噪比在接收器处测量,因为正是在这里我们试图处理信号并消除无用噪声。为了使用方便,这个比率通常用分贝表示
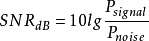 它表示有用信号超出噪声值的量,以分贝为单位。SNR的值越高,表示信号的质量越好,所需中间转发器的数量越少。
它表示有用信号超出噪声值的量,以分贝为单位。SNR的值越高,表示信号的质量越好,所需中间转发器的数量越少。
信噪比对数字数据传输十分重要,因为它限定了一个可达到的数据率上限。香农得出的结果是,用bps来表示的信道的最大容量遵从等式
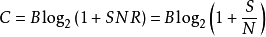
C是以比特/秒为单位的信道容量,净比特率的理论上限(信息速率,有时表示为I),不包括纠错码;
B是带宽的信道的在赫兹(通带中的带通信号的情况下的带宽);
S是以瓦(或伏平方)测量的带宽上的平均接收信号功率(在载波调制通带传输的情况下,通常表示为C);
N是噪声和带宽上的干扰的平均功率,以瓦(或伏特平方)为单位测量;
S / N是通信信号对接收机噪声和干扰的信噪比(SNR)或载波噪声比(CNR)(表示为线性功率比,而不是对数分贝) 。
香农公式显示出理论上可达到的最大值。然而在实际应用中能够达到的速率要低得多。其中一个原因是该公式假定噪声为白噪声(热噪声),既没有考虑到冲激噪声,也没有考虑衰减和时延失真。即使在理想白噪声情况下,因为编码的原因(如编码长度和复杂性等),目前的技术仍然无法达到香农容量。
香农公式中提到的容量为无误码容量。经香农证明,假如信道上的实际信息率比无误码容量低,从理论上来说,通过适当的信息编码,信道就有可能达到无误码容量。遗憾的是,香农的理论并没有给出如何找到这种编码的方法,但提供了一个用来衡量实际通信机制性能的计算标准。
通过香农公式我们可以考虑如何将信道容量上限提高。假如噪声值给定,那么似乎通过增加信号强度或带宽就能提高数据率;但是,如果信号强度增加了,则系统的非线性程度也会提高,这就导致互调噪声的增加。还有一点需要注意,由于假定噪声是白噪声,那么带宽越宽,因此系统容纳的噪声也就越多,因此随着B的增加SNR反而降低了。
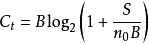
当 ,或
,或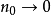 时,
时,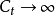 。
。
但是当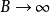 时,
时, 将趋向何值?
将趋向何值?
令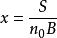 ,上式可以改写为:
,上式可以改写为:
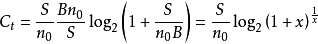
利用关系式:

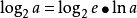
上式变为:
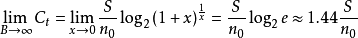
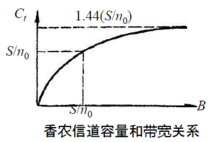
上式表明,当给定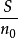 时,若带宽B趋于无穷大,信道容量不会趋于无限大,而只是
时,若带宽B趋于无穷大,信道容量不会趋于无限大,而只是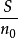 的1.44倍。这是
的1.44倍。这是
因为当带宽B增大时,噪声功率也随之增大。
 和带宽B的关系曲线:
和带宽B的关系曲线:
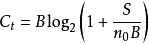 上式还可以改写成如下形式:
上式还可以改写成如下形式:
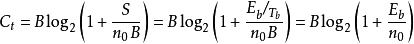 式中
式中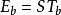 ——每比特能量
——每比特能量
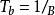 ——每比特持续时间
——每比特持续时间
上式表明,为了得到给定的信道容量 ,可以增大带宽B以换取
,可以增大带宽B以换取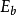 的减小;另一方面,在接收功率受 限的情况下,由于
的减小;另一方面,在接收功率受 限的情况下,由于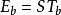 ,可以增大
,可以增大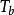 以减小S来保持
以减小S来保持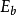 和
和 不变。
不变。
香农定理与香农限香农定理概述在信息理论中,噪声信道编码定理(有时是香农定理)确定了对于通信信道的任何给定程度的噪声污染,可以将几乎无错误的离散数据(数字信息)传送到可计算的最大值通过渠道率。这个结果由克劳德·香农在1948年提出,部分原因是早期的工作和哈里·奈奎斯特(Harry Nyquist)和拉尔夫·哈特利(Ralph Hartley)的观点。
香农定理指出,给定具有信道容量C和以速率R发送的信息的噪声信道,则if R C,任意小的错误概率是无法实现的。所有代码将具有大于某个正极小水平的误差概率,并且该水平随着速率的增加而增加。因此,不能保证通过信道容量以外的速率可靠地传输信息。定理没有解决速度和能力相等的罕见情况。
信道容量C可以根据信道的物理性质来计算;
数学概述
对于每个离散的无记忆通道,通道容量
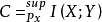
具有以下属性。对于任何ε> 0且- [R > 1,那么
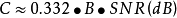 这里
这里
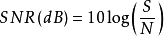
2. 同理,如果S / N




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国