[科普中国]-多面体运算

多面体的运算(operations of polytopes)是多面体间的变换，即由两个多面体对应出一个新多面体的映射1。

多面体之和多面体之和(sum of polytopes)是多面体P1和P2之和，记为

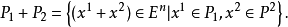多面形的分解定理使用的正是此类运算。

相邻多面体的和是相邻多面体的一种合成，即由相邻多面体导出的一个多面体，两个相邻多面体，剔除其所有的公共点后，所形成的第三个多面体，称为两个相邻多面体的和。

凸多面形分解定理亦称法尔卡斯-闵科夫斯基-外尔定理，反映线性不等式组解集结构的一个命题，由非齐次联立不等式组之解集构成的凸多面形可做如下分解：P=M+K(“+”的意义为“多面体之和”)，其中M为凸多面体，K为由齐次联立不等式组之解集构成的凸多面锥，此定理把凸多面形分解为相对简单的凸多面体和凸多面锥，从而给多面形的处理带来方便，例如，线性规划理论的基本定理是得益于此分解定理1。

多面体之积多面体P1和P2之积记为

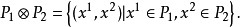
多面体之极多面体P的极记为

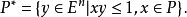
当P为单点元素a时，P为En中的半空间：

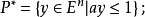
当P为单点元素O时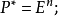，当P为半空间时，P为线段或射线1。

多面体投影像多面体投影像(projective image of polytope)是一类多面体运算，从Ed到Ek的投影映射

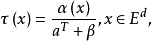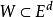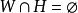其中α为从Ed到Ek的仿射映像，a是一个d维向量，β是一个实数，T表示向量的转量。对于一个集合，若，其中

则称τ对W为可行的，若τ是一个投影映射并且对于多面体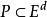为可行的，则称τ(P)为多面体P的投影像1。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所