[科普中国]-基本最优解

基本最优解(basic optimal solution)是线性规划的重要概念，指线性规划问题中使目标函数达到最优值的基可行解。

基本介绍考虑标准型LP问题

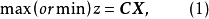
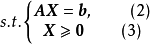
设A是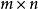阶矩阵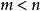，，且A的秩为m。

可行解：满足上述约束条件(2)、(3)的向量x称为可行解(feasible solution)。

最优解：满足式(1)的可行解称为最优解(optimal solution)。

基：A中任何一组m个线性无关的列向量构成的子矩阵B，称为该问题的一个基(basis)，即B为A的m×m阶非奇异子矩阵。

基向量：基B中的一列即为B的一个基向量。基B中共有m个基向量。

非基向量：矩阵A中基B之外的一列即为B的一个非基向量。A中共有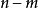个非基向量。

基变量：与基B的基向量相应的变量称为B的基变量。基变量共有m个。

非基变量：与基B的非基向量相应的变量称为B的非基变量，非基变量共有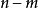个。

基本解：对于基B，令所有非基变量为零，求得满足式(2)的解，称为B对应的基本解(basic solution)。

基本可行解：满足式(3)的基本解称为基本可行解，其对应的基称为可行基。

基本最优解：满足式(1)的基本可行解称为基本最优解，其对应的基称为最优基。

退化的基本解：若基本解中有基变量为零者，则称之为退化的基本解。类似地，有退化的基本可行解和退化的基本最优解1。

求解方法单纯形方法是求解线性规划问题的一个主要方法，构成了线性规划理论的一个重要内容，其计算主要是由单纯形表来实现的。

设线性规划目标函数为：

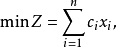约束条件为：

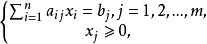其矩阵形式为：

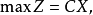
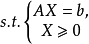令，其中B是秩为m的m阶方阵，

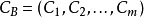
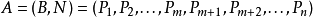那么称，

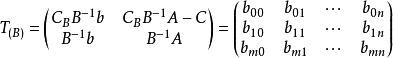基B对应的单纯形表。

表中第1列第1分量是对应于B基础解即的目标函数值，其他m个分量就是对应于B的基础解中基变量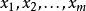的值。表中第1行除第1分量外，其余n个分量为检验数CBB-1A—C。对于可行基B(即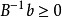)的表，如果所有检验数非正，那么这一基础可行解就是最优解。第1个可行基一般取单位矩阵，这只要在约束方程两边同乘以+1或-1，并引入和方程个数相同的人工变量，那么这m个人工变量对应的系数矩阵就是单位矩阵Im，且满足。

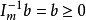如果有一个检验数大于零，那么就需要换基迭代，其步骤是：(1)求主元素。在所有中，选最靠左的一个，记为b0s，其对应的非基变量xs，对应于向量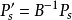，用P's列正的各分量bis分别去除bi0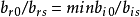，，称brs为主元素。(2)对B的单纯形表进行变换使P's变为单位向量(第r个分量为1，其余为0)，将P's与第r列对调，即将一个新基的单纯形表。那么换基后目标函数值不会增加，只有在下述情形原问题无最优解：检验数b0j中有正数，且无对应的列向量是负向量2。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所