[科普中国]-正定二次函数

正定二次函数(positive definite quadratic function)是系数矩阵为对称正定矩阵的二次函数。设x∈Rn，A为n×n对称正定矩阵，b∈Rn为常向量，c为常数，则二次函数f(x)=1/2xTAx+bTx+c称为正定二次函数1。

基本介绍二次函数是最简单的非线性函数，在最优化理论中具有重要的意义。根据函数的泰勒二次展开式，可以把一般的二次函数写成以下向量形式：

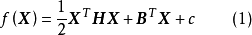式中，B为常数向量，相当于函数的梯度；H为n×n阶常数矩阵，相当于函数的二阶导数矩阵。 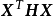称二次型，H称二次型矩阵2。

矩阵有正定、负定和不定之分。对于任意非零向量X：

(1) 若有 ，则称矩阵且H是正定矩阵。

(2)若有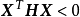 ，则称矩阵H是负定矩阵。

(3)若有时 ，有时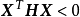 ，则称矩阵H是不定矩阵。

由线性代数可知，矩阵H的正定性除了可以用上面的定义判断外，还可以用矩阵的各阶主子式进行判别。所谓矩阵的主子式，就是包含第一个元素在内的左上角各阶子矩阵所对应的行列式。

如果矩阵H的各阶主子式的值均大于零，即

一阶主子式

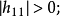
二阶主子式

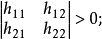
三阶主子式

则矩阵H是正定的。

如果矩阵H的各阶主子式的值负正相间，即

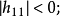
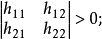
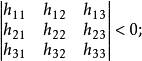
即奇数阶主子式小于零，偶数阶主子式大于零时，矩阵H负定，否则H不定。

如果式(1)中的二次型矩阵H是正定的，则称函数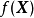 为正定二次函数2。

性质介绍在最优化理论中正定二次函数具有特殊的作用，这是因为许多最优化理论和最优化方法都是根据正定二次函数提出并加以证明的，而且所有对正定二次函数适用并有效的最优化算法，经证明，对一般非线性函数也是适用和有效的。

可以证明，正定二次函数具有以下性质：

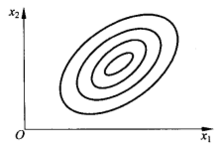
(1)正定二次函数的等值线(面)是一族同心椭圆(球)。椭圆(球)族的中心就是该二次函数的极小点，如图1所示。

(2)非正定二次函数在极小点附近的等值线(面)近似于椭圆(球)，如图2所示2。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所