映射芽(germ of mapping)是奇点理论与突变理论的主要研究对象之一。确定在一点的邻域上的连续映射的等价类,精确地说,设X,Y是拓扑空间,p∈X,考虑由在点p附近定义的全体连续映射g所构成的集合A,A={g|g:U→Y,U是点p的开邻域,g是连续映射},在这个集合里引进等价关系如下:设g:U→Y,f:V→Y是A中的两个映射,若存在点p的开邻域W,使得W⊂U∩V,而且f和g在W上的限制相等,即f|W=g|W,则称f和g等价,在这个等价关系下的一个等价类就称为映射在点p的芽,常记为h:(X,p)→Y,这个类中的任何映射g都称为芽h的代表,而h也称为映射g在点p的芽,关于映射的许多概念,如两个映射的复合映射等都可以自然的方式搬到映射芽上来,特别地,函数的相乘、相加等概念能够以自然的方式搬到函数芽上,在奇点理论与突变理论中研究的是可微映射芽1。
映射芽的接触等价映射芽的接触等价是奇点理论的一个概念,它是反映两个映射的零点集局部拓扑等价的概念.设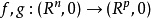 是两个可微映射芽,若存在C微分同胚芽
是两个可微映射芽,若存在C微分同胚芽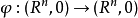 和可微映射芽
和可微映射芽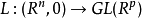 ,这里GL(R)是一般线性群,
,这里GL(R)是一般线性群,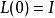 ,I为R上的恒等变换,使得
,I为R上的恒等变换,使得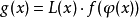 ,则称f和g是C接触等价的。若φ与L均为Cr可微映射芽,则称f与g是C接触等价的,当φ与L仅为连续时,就称f与g是C0接触等价的,或称为拓扑接触等价的,若f与g是
,则称f和g是C接触等价的。若φ与L均为Cr可微映射芽,则称f与g是C接触等价的,当φ与L仅为连续时,就称f与g是C0接触等价的,或称为拓扑接触等价的,若f与g是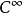 接触等价,则局部微分同胚芽φ把
接触等价,则局部微分同胚芽φ把 在点O的芽映成
在点O的芽映成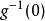 在点O的芽,于是,f与g是
在点O的芽,于是,f与g是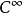 接触等价的当且仅当存在一
接触等价的当且仅当存在一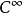 微分同胚芽
微分同胚芽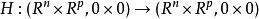 使得:
使得:
1.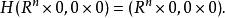
2.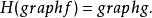
用K记由所有满足下面条件的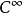 微分同胚芽
微分同胚芽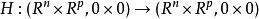 相对于结合映射运算做成的群,这里关于H存在可微映射芽
相对于结合映射运算做成的群,这里关于H存在可微映射芽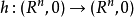 ,使得下图交换
,使得下图交换
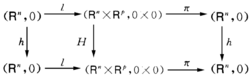
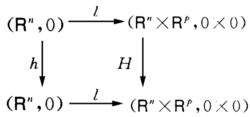

这里l为嵌入映射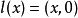 ,π为投影映射.群K在
,π为投影映射.群K在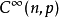 上的作用由下式刻画:
上的作用由下式刻画: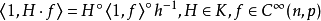 ,1记恒同映射芽:
,1记恒同映射芽: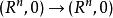 ,从而,f与g是接触等价的当且仅当f与g属于群K作用下的同一个轨道1。
,从而,f与g是接触等价的当且仅当f与g属于群K作用下的同一个轨道1。
映射芽的决定性映射芽的决定性(determinacy of map-germs)是反映映射在一点的局部性质,它可以由其在该点的某些导数所决定.。设N,P为光滑流形,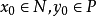 ,CN表示由无穷次可微函数芽
,CN表示由无穷次可微函数芽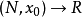 的全体构成的集合,
的全体构成的集合,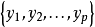 表示y0的局部坐标,
表示y0的局部坐标,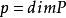 ,设M为
,设M为
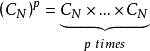 的R线性子空间,给定一个无穷次可微映射芽
的R线性子空间,给定一个无穷次可微映射芽 ,若存在可微映射芽
,若存在可微映射芽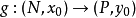 使得
使得
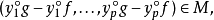 则称g是f的M逼近,若对于f的每个M逼近g,f和g关于右-左等价关系都是
则称g是f的M逼近,若对于f的每个M逼近g,f和g关于右-左等价关系都是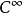 等价的,则称f是M决定的,注意,在一般情况下,f的M决定性与点y0的局部坐标的选取有关,但是,当M是CN的某个理想I的p次直积时,就与坐标系的选取无关1。
等价的,则称f是M决定的,注意,在一般情况下,f的M决定性与点y0的局部坐标的选取有关,但是,当M是CN的某个理想I的p次直积时,就与坐标系的选取无关1。
映射芽的右-左等价映射芽的右-左等价是两个映射之间的一种关系,指两个映射经过其定义域及值域的坐标变换后可以把一个变为另一个.,设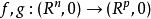 是两个可微映射芽,若存在
是两个可微映射芽,若存在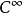 微分同胚芽
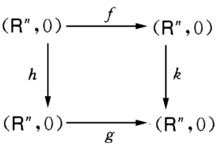
微分同胚芽 和k:(R,0)→(R,0),使得右图交换,即k°f=g°h,则称映射芽f与g是C右-左等价的,若h,k都是C微分同胚芽,则称f与g是C右-左等价的,若h,k仅是同胚芽,则称f与g是拓扑右-左等价的,记A=R×L(群R,L的定义参见“映射芽的右等价”和“映射芽的左等价”).群A自然地作用在
和k:(R,0)→(R,0),使得右图交换,即k°f=g°h,则称映射芽f与g是C右-左等价的,若h,k都是C微分同胚芽,则称f与g是C右-左等价的,若h,k仅是同胚芽,则称f与g是拓扑右-左等价的,记A=R×L(群R,L的定义参见“映射芽的右等价”和“映射芽的左等价”).群A自然地作用在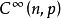 上,这里
上,这里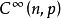 记
记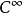 可微映射芽
可微映射芽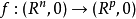 之全体,即
之全体,即
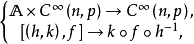 f与g右-左等价当且仅当存在(h,k)∈A使
f与g右-左等价当且仅当存在(h,k)∈A使
 亦即f与g属于群A作用下的同一个轨道。
亦即f与g属于群A作用下的同一个轨道。
本词条内容贡献者为:
王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国