[科普中国]-模糊关系方程

模糊关系方程(fuzzy relation equation;FRE)是含有未知模糊关系的一类等式。设X与Y为有限论域，A是X上的模糊子集，R为X到Y的模糊关系，则可通过复合运算得到Y上的模糊子集B=A°R，若已知B与R，欲求A；或已知B与A，求R，使满足A°R=B，则称该等式为模糊关系方程。所求出的A或R称为该模糊关系方程的解。一般地，模糊关系方程的解不是惟一的，桑切斯(E.Sanchez)首先研究了模糊关系方程，指出模糊关系方程存在最大解和极小解，但一般不存在最小解1。

基本介绍模糊关系方程在模糊数学理论及其应用中占有十分重要的地位。法国的桑切斯在这方面做了开创性的研究。他最早提出模糊关系方程并且给出了方程的最大解。继之日本的政元对有限集上模糊关系方程的求解给出具体解法，我国的罗承忠、徐文立、曹志强、李必祥等给出了方程的简化解法。

模糊关系方程的种类模糊关系方程有两种类型。

类型Ⅰ给定论域U、V、W，已知模糊关系

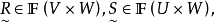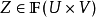求模糊关系满足方程：

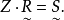
类型Ⅱ已知模糊关系

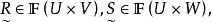求模糊关系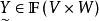，满足方程：

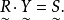
在类型Ⅱ中，令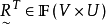，其隶属函数：

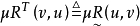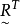称为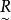的转置关系，同样规定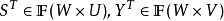，则T满足方程：

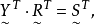因而，两种类型的方程可以互相转化。

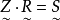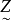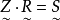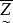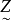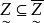模糊关系方程解满足模糊关系方程的称为方程的解，如果方程有解，则称方程为相容的，否则称方程为不相容的。如果方程的某个解，对其他任何一个解，恒有，则称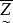为方程的最大解。

桑切斯最一般地证明了，对任意模糊关系方程，若有解则必有最大解。对有限论域上的模糊关系方程，政元给出了具体解法，称为政元方法。罗承忠等对政元方程进行了简化2。参见模糊关系。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所