模糊线性规划(fuzzy linear programming)是经典线性规划的一种推广,它是将线性约束的边界模糊化,从而使人们能在较宽松的条件下求得优化的条件与优化的极值1。
基本介绍自从1970年,Bellman与Zadeh提出模糊决策的概念之后,模糊优化一直是一个引人注目的研究领域。在这个领域中模糊线性规划是一个发展较为成熟的领域,特别是用以求解模糊线性规划的容差法(Tolerance Approach),不仅理论上比较完备,也在实际模糊决策中获得了广泛应用。
线性规划已经广泛地用于现代物流调运、资源优化配置、组合投资分析、区域经济规划等经济领域。由于普通线性规划的约束条件是固定的,在经济发展过程中必然会出现一些波动,因此实际问题需要约束条件具有一定的弹性,目标函数可能不是单一的,可以借助于模糊集合的方法来处理。引入隶属函数概念,将线性规划的约束条件与目标函数模糊化,进而导出一种新的线性规划问题,它的最优解称为原问题的模糊最优解。
对于通常的线性规划问题,即在约束条件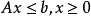 下,求目标函数
下,求目标函数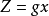 的极值min Z,考虑约束条件的软化
的极值min Z,考虑约束条件的软化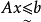 ,
, ,这里“
,这里“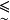 ”表示对“≤”的一种放宽,并确定它的隶属函数为
”表示对“≤”的一种放宽,并确定它的隶属函数为
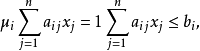
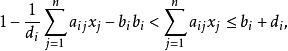
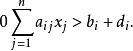 这即是模糊线性规划问题1。
这即是模糊线性规划问题1。
模糊线性规划的模型模糊约束线性规划的一般形式如下2:
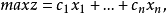
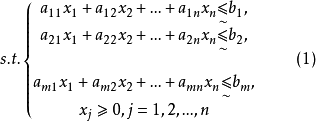 模糊线性规划的模型可简记为:
模糊线性规划的模型可简记为:
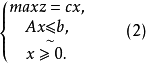
模糊线性规划的求解下面我们来讨论式(2)的求解问题2。
设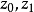 分别是普通线性规划,即
分别是普通线性规划,即
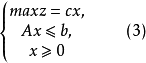
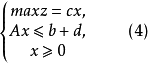 的最优值,其中
的最优值,其中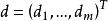 称为式(2)的伸缩指标向量。
称为式(2)的伸缩指标向量。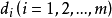 为第i个伸缩指标。
为第i个伸缩指标。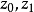 对应两种极端情况,一种是完全接受约束
对应两种极端情况,一种是完全接受约束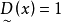 ),另一种是完全不接受约束(
),另一种是完全不接受约束(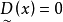 ),它们都不是我们所希望的。我们的目的是适当减低隶属度
),它们都不是我们所希望的。我们的目的是适当减低隶属度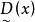 ,使得最优值有所提高且介于
,使得最优值有所提高且介于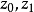 之间,为此构造模糊目标集
之间,为此构造模糊目标集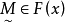 ,其隶属度为
,其隶属度为
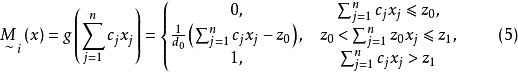 其中,
其中,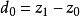 。易见,当
。易见,当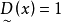 时,
时,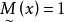 ,这表明欲使目标值大于z0,必须降低
,这表明欲使目标值大于z0,必须降低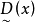 。为了兼顾模糊约束集
。为了兼顾模糊约束集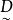 与模糊目标集
与模糊目标集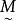 ,可采用模糊判决
,可采用模糊判决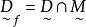 ,然后选择
,然后选择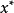 ,使
,使
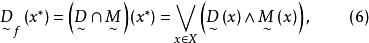 注意到
注意到
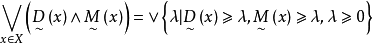
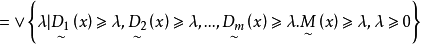 于是问题归结为求普通线性规划问题,若求出普通线性规划问题的最优解为
于是问题归结为求普通线性规划问题,若求出普通线性规划问题的最优解为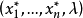 ,则
,则
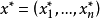 为式(3)的最优解,得式(3)的最优解
为式(3)的最优解,得式(3)的最优解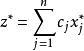 。2
。2
本词条内容贡献者为:
王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国