[科普中国]-非平凡分解

若亚纯函数F的分解形式中每一个因子关皆为非双线性亚纯函数时，则称之为一非平凡分解。

简介亚纯函数因式分解亚纯函数因式分解是亚纯函数在复合意义下的分解。

设F(z)为一亚纯函数，若F(z)可表为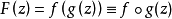，f，g为亚纯函数；或一般地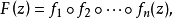fi(z) (1≤i≤n)皆为亚纯函数，以上两个等式皆称为F的因式分解或称分解。

非平凡分解特别地，若F的分解形式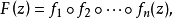中每一个因子关皆为非双线性亚纯函数时，则称之为一非平凡分解。

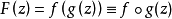的分解中，f称为左因子，g 称为右因子。1

亚纯函数亚纯函数是在区域D上有定义，且除去极点之外处处解析的函数。在复分析中，一个复平面的开子集D上的亚纯函数是一个在D上除一个或若干个孤立点集合之外的区域全纯的函数，那些孤立点称为该函数的极点。每个D上的亚纯函数可以表达为两个全纯函数的比（其分母不恒为0）：极点也就是分母的零点。

直观的讲，一个亚纯函数是两个性质很好的（全纯）函数的比。这样的函数本身性质也很“好”，除了分式的分母为零的点，那时函数的值为无穷。

从代数的观点来看，如果D是一个连通集，则亚纯函数的集合是全纯函数的整域的分式域。这和有理数Q和整数Z的关系类似。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所