[科普中国]-贝塞尔滤波器

贝赛尔(Bessel)滤波器是具有最大平坦的群延迟（线性相位响应）的线性过滤器。贝赛尔滤波器常用在音频天桥系统中。模拟贝赛尔滤波器描绘为几乎横跨整个通频带的恒定的群延迟，因而在通频带上保持了被过滤的信号波形。滤波器的名字来自于Friedrich贝赛尔，一位德国数学家（1784–1846），他发展了滤波器的数学理论基础。

简介贝塞尔(Bessel)滤波器具有最平坦的幅度和相位响应。带通（通常为用户关注区域）的相位响应近乎呈线性。Bessel滤波器可用于减少所有IIR滤波器固有的非线性相位失真。

贝塞尔(Bessel)线性相位滤波器正是由于具有向其截止频率以下的所有频率提供等量延时的特性，才被用于音频设备中，在音频设备中，必须在不损害频带内多信号的相位关系前提下，消除带外噪声。另外，贝塞尔滤波器的阶跃响应很快，并且没有过冲或振铃，这使它在作为音频DAC输出端的平滑滤波器，或音频ADC输入端的抗混叠滤波器方面，是一种出色的选择。贝塞尔滤波器还可用于分析D类放大器的输出，以及消除其它应用中的开关噪声，来提高失真测量和示波器波形测量的精确度。

虽然贝塞尔滤波器在它的通频带内提供平坦的幅度和线性相位（即一致的群延时）响应，但它的选择性比同阶（或极数）的巴特沃斯(Butterworth)滤波器或切比雪夫(Chebyshev)滤波器要差。因此，为了达到特定的阻带衰减水平，需要设计更高阶的贝塞尔滤波器，从而它又需要仔细选择放大器和元件来达到最低的噪声和失真度。1

传递函数描述贝塞耳滤波器低通滤波器的传递函数如下：

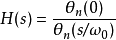
这里θn(s)是一个反向贝塞耳多项式，ω0是选定的期望截止频率。

简单例子下面是一个三阶贝塞尔低通滤波

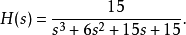
gain值为

相位为

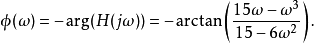
群延迟为

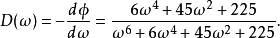
群延迟的泰勒级数展开为

注意在ω2和ω4的二个项是零，在ω=0造成非常平坦的群延迟。这是可以调整到零项的最大数量，因为在三阶贝赛尔多项式中总共有四个系数，要求定义四个等式。一个等式是为了在ω = 0 时，结果是统一的。第二个等式指定ω =无穷时结果是零，剩下二个等式指定二个项的级数展开是零。这是n秩贝赛尔滤波的群延迟的一般特性：在群延迟的前n-1级数展开的项为零，因而ω = 0时群延迟的扁平得以最大化。

特性贝塞尔滤波器的相移与频率关系如图一所示。

从图上可以看出，贝塞尔滤波器带来的延时，基本是线性的，保证了滤波后的信号波形的完整性，贝塞尔滤波器在通频带内，其幅度特性也较为平坦，如图二所示。

但是与相同阶数的巴特沃斯、切比雪夫滤波器相比，贝塞尔滤波器在信号衰减方面有劣势，其阻带下降响应速度过慢，所以一般设计成高阶数的滤波器来达到相应的阻带衰减水平。

贝塞尔滤波器在通频带范围内，有近似的线性时延特性和较平坦的幅度特性，保证了信号处理的准确性及信号的无畸变传输，从而使贝塞尔滤波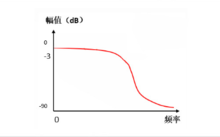器常用作音频系统ADC输入之前的抗混叠滤波器以及DAC输出端的平滑滤波器。在生物医学信号放大与处理过程中也得到广泛的应用。2

本词条内容贡献者为:

曹慧慧 - 副教授 - 中国矿业大学