牛顿方向(Newton direction)是求解无约束最优化问题中的一个概念,指向二次函数最优点的方向,对于Rn上的非二次函数f,设f在Rn中二次连续可微,点xk⊂Rn,▽f(xk)是f在xk处的梯度,H(xk)是f在xk处的黑塞矩阵,则f在xk处的牛顿方向是-H(xk)-1▽f(xk)。1
基本介绍考虑目标函数f在点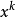 处的二次逼近式
处的二次逼近式
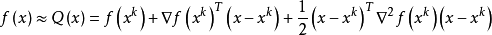 假设Hesse阵
假设Hesse阵
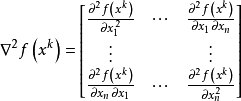 正定。
正定。
由于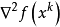 正定,函数Q的稳定点
正定,函数Q的稳定点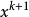 是Q(x)的最小点。为求此最小,令
是Q(x)的最小点。为求此最小,令
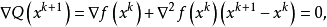 即可解得
即可解得
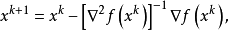 可知从点
可知从点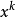 出发沿搜索方向,即
出发沿搜索方向,即
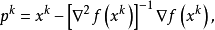 并取步长
并取步长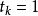 即可得Q(x)的最小点
即可得Q(x)的最小点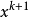 。通常,把方向
。通常,把方向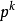 ‘称为从点
‘称为从点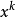 出发的牛顿方****向。从一初始点开始,每一轮从当前迭代点出发,沿牛顿方向并取步长为1的求解方法,称为牛顿法2。
出发的牛顿方****向。从一初始点开始,每一轮从当前迭代点出发,沿牛顿方向并取步长为1的求解方法,称为牛顿法2。
相关分析设
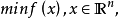
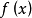 在点
在点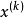 处具有二阶连续偏导数,且在点
处具有二阶连续偏导数,且在点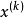 处的黑塞矩阵
处的黑塞矩阵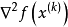 定,
定,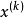 是
是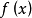 的一个极小点的第k轮估计值。
的一个极小点的第k轮估计值。
将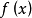 在
在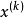 处作二阶泰勒展开:
处作二阶泰勒展开:
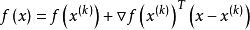
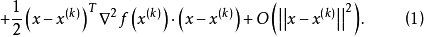 又记
又记
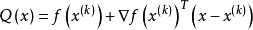
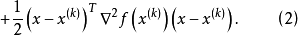 注意到
注意到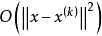 是比
是比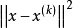 高阶的无穷小量,故有
高阶的无穷小量,故有
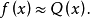 下面来求Q(x)的平稳点:
下面来求Q(x)的平稳点:
记
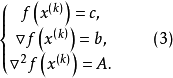 其中c为数,b为向量,A为矩阵,将(3)式代入(2)式,则
其中c为数,b为向量,A为矩阵,将(3)式代入(2)式,则
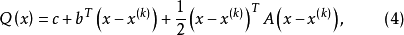 且
且
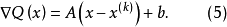 令
令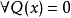 ,记
,记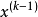 为Q(x)的平稳点,则有
为Q(x)的平稳点,则有
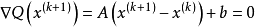 或
或
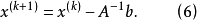 将(3)式代入上式,有
将(3)式代入上式,有
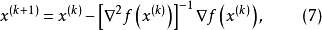 记
记
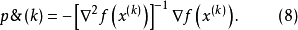 代人(7)式有
代人(7)式有
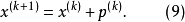 称由(8)式决定的搜索方向
称由(8)式决定的搜索方向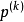 为牛顿方向。3
为牛顿方向。3
牛顿方向的几何意义下面来分析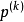 的几何意义。
的几何意义。
因为Q(x)是一个二次函数,且有
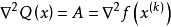 是一个正定矩阵,因此Q(x)是凸函数,则其平稳点即是全局极小点,即
是一个正定矩阵,因此Q(x)是凸函数,则其平稳点即是全局极小点,即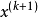 是Q(x)的极小点,由(9)式:
是Q(x)的极小点,由(9)式:
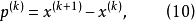 (10)式表明了由(8)式确定的方向
(10)式表明了由(8)式确定的方向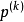 实质上是由
实质上是由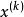 指向
指向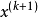 的方向,即由
的方向,即由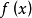 的第k轮极小点估计值指向近似二次函数Q(x)的极小点的方向。
的第k轮极小点估计值指向近似二次函数Q(x)的极小点的方向。
由(8)式确定的搜索方向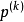 ,及由(9)式确定的下一个迭代点
,及由(9)式确定的下一个迭代点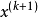 ,是牛顿法算法的主要内容,由(9)式可看出,牛顿法实际上已规定步长因子为1。3
,是牛顿法算法的主要内容,由(9)式可看出,牛顿法实际上已规定步长因子为1。3
本词条内容贡献者为:
武伟 - 高级工程师 - 天津直升机有限责任公司




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国