[科普中国]-玛尔格朗日预备定理

在数学中，玛尔格朗日预备定理是Weierstrass准则定理的类似，用于平滑函数。 它由RenéThom推测并由B. Malgrange证明（1962-1963,1964,1967）。

陈述假设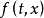是原点附近的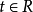和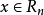的平滑复函数，并且令k为最小整数，使得

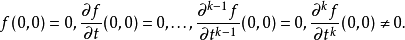
然后，准备定理的一种形式表明，原点f附近可以写为在原点处非零的平滑函数c和作为t的函数的平滑函数的乘积是k的多项式。 换一种说法，

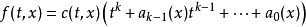函数c和a是平滑的，c在原点是非零的。

定理的第二种形式，偶尔称为马瑟分裂定理，是一种“余数除法”定理：它说如果f和k满足上述条件而g是原点附近的平滑函数，那么我们就可以写

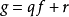
其中q和r是平滑的，并且作为t的函数，r是小于k的多项式。这意味着

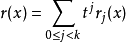对于一些平滑函数。

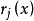定理的两种形式容易相互暗示：第一种形式是“余数除法”形式的特殊情况，其中g是tk，而余数形式的除法遵循定理的第一种形式，因为我们可以假设作为t的函数的f是k次多项式。

如果函数f和g是实数，那么函数c，a，q和r也可以被认为是真实的。在Weierstrass准备定理的情况下，这些函数由f和g唯一确定，但对于玛尔格朗日预备定理，唯一性不再适用1。

定理的证明玛尔格朗日预备定理可以从Weierstrass预备定理推导出来。这样做的明显方法不起作用：虽然平滑函数在原点具有正式的幂级数展开，而Weierstrass预备定理适用于形式幂级数，但形式幂级数通常不会收敛到原点附近的平滑函数。相反，人们可以通过将单位分区应用于其傅立叶变换来使用将平滑函数分解为解析函数之和的思想。有关这些方面的证据，请参阅(Mather 1968)或 (Hörmander 1983a, 第7.5节）

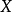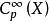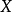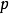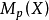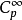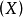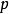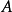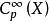代数版的玛尔格朗日预备定理玛尔格朗日预备定理可以作为关于平滑，实值细菌环的模块的定理来重述。如果是具有的流形，则让表示在上的处的平滑函数的实值细菌的环。设表示的唯一最大理想，由在消失的细菌组成。设是 - 模，让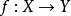是流形之间的平滑函数。设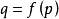。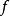通过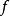右侧的组合诱导环同态 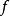*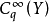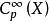：→。因此，我们可以将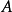视为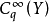模块。然后玛尔格朗日预备定理说如果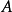是有限生成的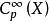模块，则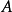是有限生成的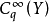模块，当且仅当 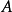/ 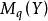是有限维实数向量空间。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学