[科普中国]-切面距离算法

针对传统欧几里得距离存在的问题，切面距离算法假设待分类的样本和处于同一个流形上的样本具有相同的类别，根据邻近流形关于聚集概率的知识导出距离度量，是一种非参数的最近邻算法。

问题提出在模式识别中，一种简单但效率低下的方法是使用简单的距离测量，例如表示原始输入矢量之间的欧几里德距离。这种方法效率很低，因为几乎所有类别的实例都必须存在于原型集中，例如，在手写数字识别中，必须存储所有可能出现位置、大小、角度、书写样式、线条粗细和倾斜的每个类的数字。在实际情况中，这种方法导致不切实际的原型集或普通的识别准确性。

如图1，一个宽线条的、倾斜的“9”的待标记图像必须通过从两个图像中找到最接近的原型图像来分类，这两个图像分别代表一个线条细的、直立的“9”和一个线条粗的、倾斜的“4”。根据欧几里德距离，“4”和待标记图像更接近，但却不是正确的分类。

处理这类问题的经典方法是使用特征提取器，其目的是计算模式的特征表示，对于字符识别，特征表示应在位置，尺寸变化，轻微旋转，扭曲或线条厚度变化方面不变。特征提取器的设计和实现是构建模式识别系统的主要瓶颈。

另一种方法是使用不变距离测量，以这种方式构造原型和模式之间的距离不受模式或原型的无关变换的影响。 通过不变距离测量，每个原型可以匹配许多可能的模式实例，从而大大减少了所需的原型数量。1其关键思想是构建一个距离度量，该度量对于某些选定的变换（例如平移，旋转等）是不变的。2

切面距离切面距离算法包括计算非线性流形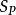和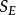的最佳近似线性表面之间的最小距离。它主要解决了三个问题：

(1) 线性流形具有简单的解析表达式，可以很容易地计算和存储；

(2) 找到线性流形之间的最小距离是一个可以有效求解的简单最小二乘问题；

(3) 这个距离是局部的，而不是全局的、不变的。

因此，“6”和稍旋转的“6”之间的距离很小，但“6”和“9”之间的距离很大。P和E之间的不同距离示意图如图2。

细节切面距离算法是一种非参数的最近邻算法，其使用的度量不是通用的欧几里德距离，而是根据邻近流形关于聚集概率的知识导出的。该算法假设待分类的样本和处于同一个流形上的样本具有相同的类别。由于分类器应该对局部因素（对应于流形上的移动）的变化保持不变，一种合理的度量是将点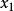 和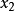 各自所在流形 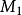和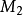的距离作为点 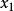和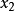 之间的最近邻距离。然而这可能在计算上是困难的（它需要解决一个寻找 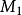和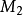 最近点对的优化问题），一种局部合理的廉价替代是使用 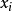点处切平面近似 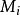，并测量两条切平面或一个切平面和点之间的距离。这可以通过求解一个低维线性系统（就流形的维数而言）来实现。当然，这种算法需要指定那些切向量。3

本词条内容贡献者为:

刘燕兵 - 副研究员 - 中国科学院信息工程研究所