[科普中国]-亏量关系

由第二基本定理可得下述重要的亏量关系，即至多有可数个亏值，且总亏量满足亏量之和小于等于2。

简介亏值设w(z)为复平面C上的亚纯函数，定义w(z)关于a的亏量为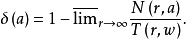如果δ(a)>0，则称a为亏值。

亏量关系由第二基本定理可得下述重要的亏量关系，即至多有可数个亏值，且总亏量满足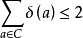。1

第二基本定理第二基本定理是亚纯函数奈望林纳理论中重要定理。

设w(z)为亚纯函数，ak(k=1,2,...,p)是p(>2)个互异的复数（有穷或无穷），则有第二基本定理如下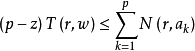：其中N1(r,w)是重值点数目函数，S(r,w)为余项，满足S(r,w)=O(logrT(r,w))(r→∞)。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学