[科普中国]-外尔斯特拉斯第一定理

外尔斯特拉斯第一定理可看成是多项式因子分解定理的推广，是关于整函数因子分解的重要定理，是1876年由外尔斯特拉斯（Weierstrass,K.(T.W.)）提出的。

简介外尔斯特拉斯第一定理是关于整函数因子分解的重要定理，是1876年由外尔斯特拉斯（Weierstrass,K.(T.W.)）提出的。

定理定理叙述如下：设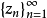是整函数f(z)的异于零的零点序列，且满足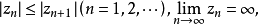每一零点在序列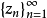中出现的次数与其重级相同，又设为正整数序列，它使得级数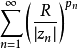对任意的R>0收敛，则无穷乘积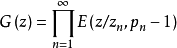对任意的复数z绝对收敛，且f(z)能表示为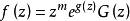，其中g(z)为另一整函数，m≥0为整数。

应用外尔斯特拉斯第一定理可看成是多项式因子分解定理的推广，但多项式情形能由其零点惟一地确定（除去一个常数因子），而一般超越整函数只能确定到任意一个不取零值的整函数因子，而且为保证无穷乘积的收敛性，需要引入基本因子。1

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学