[科普中国]-量子傅里叶变换

量子傅里叶变换(quantum Fourier transform)是一种离散傅里叶变换，将原式分解成更为简单的多个幺正矩阵的积。

背景量子傅里叶变换实际上是作用在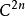空间上的离散傅立叶变换。因此学习量子傅里叶变换，我们需要先了解下离散傅里叶变换。

离散傅立叶变换是作用在复N维欧氏空间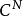上的一个酉变换，当输入为复向量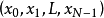时，其输出为复向量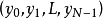，其中

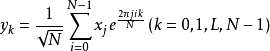
由上式得出：

概念量子傅立叶变换是进行量子力学幅度的傅立叶变换的有效量子算法，它并没有加速计算经典数据的傅立叶变换的任务，但它的一个重要任务是相位估计，即近似酉算子在某些场合的特征值。它可将原式分解成更为简单的多个幺正矩阵的积。利用这般的分解方式，离散傅里叶变换可以用作量子电路，其包含了多个哈达玛闸与受控移相闸。

量子傅里叶变换在量子算法中有多处应用1，以其可提供相位估算步骤的理论基础，在一些算法中占核心地位，例如用在做质因数分解的秀尔算法(Shor's algorithm)、顺序发现算法以及隐子群问题(hidden subgroup problem)。

公式作用在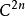空间上的离散傅立叶变换称为量子傅立叶变换。在量子计算中，称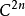空间中的元素(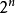维复列向量)为n量子比特。量子傅里叶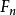有如下表达式2：

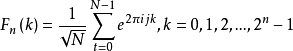
其中，N为向量的长度。注意到离散傅里叶变换是个幺正映射。

对比离散傅里叶变换和量子傅里叶变换两者的作用空间不同：前者是作用在复 N 维欧式空间的酉变换；后者是作用在复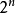维空间上的酉变换。由串行计算上升到并行计算，原来的复向量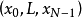变成了量子状态矩阵的其中一行，便于高速处理。但两者都可以看作是复线性空间中的酉变换。

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院