[科普中国]-二元小波转换

二元小波转换(Dyadic Wavelet Transform)是缩放以二的级数为基底且取样过后的小波转换，但时间没有取样。

背景小波变换是一种用于决定卷积的特定窗口函数，提供了将图像分解成不同尺度组成的一种数学框架1。成百种不同的小波函数被提出用来增强或模糊特定的特征。二维的离散傅里叶变换是将图像分解成不同全局正弦和余弦函数的和，而二维离散的小波变换是将一幅图像在每个尺度层上分解为四个组成部分之和。小波转换的架构分成两个部分，一个是小波分解（waveletanalysis），另一个是小波合成（wavelet synthesis）。小波分解首先要有一个原始数列的数据，这个原始数列是一个无穷数列。以影像压缩为例，数列里的每个元素的值，可以是影像中每个图点的灰阶值。有了这样的一个原始数列之后，我们要将原始数列分别进行低频分析滤波以及高频分析滤波这两个步骤。如果说我们将原始的影像，看成是由影像中具有一致性的数据以及具有高度变化性的数据，这两种数据组合而成的话，那么我们将原始数列经过低频分析滤波的步骤之后，所产生的低频数列，则将保留原始数列的一致性的数据，比如说人脸部特写的影像中，脸部会有一大片区域的颜色值相近，或者是风景照中的背景天空的一大片蓝色，就是原始资料中具有一致性的部分。而我们将原始数列经过高频分析滤波的步骤之后，所产生的高频数列，则将保留原始数列的高度变化性的数据，比如说在影像中物体的轮廓部分，边界内外的颜色值相差甚大，或者是有许多颜色参杂在一起的区域，都是原始数据中具有高度变化性的部分。因此小波分解的步骤其实就是将原始数据中的一致性数据与高度变化性数据分解成两笔独立的数据。小波合成的部分将低频数列经过低频合成滤波之后的数列，与高频数列经过高频合成滤波之后的数列，相加起来，就可以还原成原始的数列。

定义二元小波转换(Dyadic Wavelet Transform)是缩放以二的级数为基底且取样过后的小波转换，但时间没有取样。的二元小波转换的定义为2：

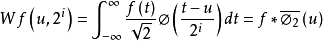
它也定义了一个稳定(stable)、完整(complete)的表示式，如果它的Heisenberg boxes囊括了所有的频率轴，也就是存在一个A和B使所有的二元小波都是L2(R)的 frame (Frames are a stable, possibly redundant, representation of signals)。

应用快速二元小波转换 (Fast Dyadic Wavelet Transform, FDWT) 使用与快速小波转换(Fast Wavelet Transform)相同的滤波器来进行转换，但是差别在于不需要再进行次采样(subsampling)，时常用在撷取音乐讯号的Onset。

Matlab实现二元小波变换的 Matlab 实现：
(1) dwt 函数
功能：离散小波变换
格式：[cA,cD]=dwt(X,'wname')
[cA,cD]=dwt(X,Lo_D,Hi_D)
说明：[cA,cD]=dwt(X,'wname') 使用指定的小波基函数 'wname' 对信号 X 进行分解，cA、cD 分别为近似分量和细节分量；[cA,cD]=dwt(X,Lo_D,Hi_D) 使用指定的滤波器组 Lo_D、Hi_D 对信号进行分解。
(2) idwt 函数
功能：离散小波反变换
格式：X=idwt(cA,cD,'wname')
X=idwt(cA,cD,Lo_R,Hi_R)
X=idwt(cA,cD,'wname',L)
X=idwt(cA,cD,Lo_R,Hi_R,L)
说明：X=idwt(cA,cD,'wname') 由近似分量 cA 和细节分量 cD 经小波反变换重构原始信号 X 。
'wname' 为所选的小波函数
X=idwt(cA,cD,Lo_R,Hi_R) 用指定的重构滤波器 Lo_R 和 Hi_R 经小波反变换重构原始信号 X 。
X=idwt(cA,cD,'wname',L) 和 X=idwt(cA,cD,Lo_R,Hi_R,L) 指定返回信号 X 中心附近的 L 个点。

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院