早在1968年, Zadeh提出了模糊事件这一概念,并在此基础上探讨了模糊事件的概率及其相关理论。
定义设(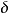 ,F,P)是概率测度空间,如果
,F,P)是概率测度空间,如果

则称A是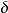 上的Fuzzy事件(fuzzy event)。
上的Fuzzy事件(fuzzy event)。
其等价定义如下:
设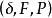 是概率测度空间,H是F上的集合套,即
是概率测度空间,H是F上的集合套,即
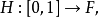
令
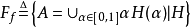 H是F上的集合套,则称
H是F上的集合套,则称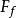 为F生成的模糊
为F生成的模糊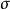 -代数,
-代数,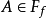 称为模糊事件1。
称为模糊事件1。
模糊概率测度设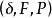 是概率测度空间,
是概率测度空间, 是F生成的模糊
是F生成的模糊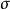 -代数,
-代数,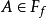 ,令
,令
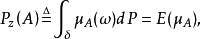
如果 是勒贝格可测的,则称
是勒贝格可测的,则称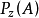 是模糊事件A的概率(probability of a event A),
是模糊事件A的概率(probability of a event A),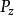 称为模糊
称为模糊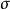 -代数
-代数 上的模糊概率测度(Fuzzy probability measure),称
上的模糊概率测度(Fuzzy probability measure),称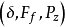 为
为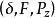 生成的模糊概率空间,即模糊事件的概率测度空间2。
生成的模糊概率空间,即模糊事件的概率测度空间2。
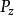 的下标Z表示
的下标Z表示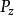 是Zadeh意义下的模糊概率测度。
是Zadeh意义下的模糊概率测度。
如果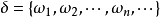 是可测集,则若记
是可测集,则若记 ,则离散型模糊事件的概率为:
,则离散型模糊事件的概率为:
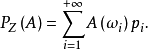
定理设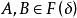 是模糊事件,则有:
是模糊事件,则有:
(1) ,且
,且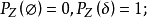
(2)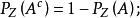
(3)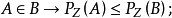
(4)
(5)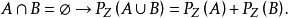
本词条内容贡献者为:
李宗秀 - 副教授 - 黑龙江财经学院




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国